第 10 章:模型优化
目标
为什么研究型优化的模型与实际部署约束之间的错配,会在机器学习系统中带来关键的工程挑战?
机器学习研究往往将“精度”置于首位,产出的模型虽然性能卓越,却难以部署到最需要它们的地方:如资源受限的移动设备、成本敏感的云环境或对延迟极为苛刻的边缘场景。模型优化正是连接理论能力与实际落地的桥梁,它将高算力消耗的研究模型转化为高效系统,在保证性能的同时满足内存、能耗、延迟和成本等多重约束。缺乏系统化的优化技术,先进的 AI 能力只能困于实验室。理解优化原理,能让工程师将复杂模型普惠到各种应用场景——从移动端运行的百亿参数大模型,到嵌入式传感器的极致部署。
学习目标
- 对比剪枝、量化、知识蒸馏、神经架构搜索等模型优化技术的原理与应用场景
- 评估不同数值精度对模型精度、能耗与硬件兼容性的权衡
- 运用三维优化框架(模型结构、数值精度、架构效率)为特定硬件设计部署方案
- 分析硬件感知设计原则如何影响模型结构决策与不同平台的计算效率
- 实践稀疏性利用与动态计算技术,在保证精度的前提下提升推理性能
- 设计集成多种优化技术的流水线,实现资源约束下的部署目标
- 评估自动化优化方法及其在超越人工调优、发现新型优化策略中的作用
模型优化基础
成功部署机器学习系统,必须解决模型复杂度与计算可行性之间的矛盾。当前机器学习研究不断产出更强大的模型,但其资源需求往往远超实际部署环境的能力。这正是将理论进步转化为可用系统的经典工程难题,直接影响 AI 应用的可及性与可扩展性。
这种资源鸿沟极为显著且多维。最前沿的语言模型,单是全精度参数存储就需数百 GB 内存,而目标平台如手机通常仅有几 GB 可用内存。这种差距不仅体现在内存,还包括算力、能耗、延迟等多方面。异构部署环境的多样性,使每种场景都提出了独特的性能约束。
生产级机器学习系统面临多目标优化难题:实时应用要求极低延迟,移动端需极致能效,嵌入式系统受限于热设计,云服务则追求大规模下的成本效益。这些约束共同构成了一个复杂的多目标优化问题,必须用系统化方法在各项性能维度上取得平衡。
模型优化定义
模型优化 指的是系统性地对机器学习模型进行变换,使其在目标部署环境下高效运行,同时保持可接受的 精度 和 功能性。该领域涵盖了在计算复杂度、内存占用、推理延迟、能效等多目标之间的权衡。常用方法包括通过参数裁剪消除冗余、通过数值精度优化降低存储和计算需求,以及通过算法和架构改进提升计算效率。模型优化让复杂的 AI 能力能在 多样化计算环境(从高性能云到资源受限的边缘设备)中落地,极大拓展了机器学习系统的实际应用范围。模型优化已从零散技巧发展为融合算法创新与硬件感知设计的系统工程学科,要求深入理解模型结构、数值精度、计算模式与硬件特性的相互作用。通过理论与实证结合,模型优化成为有据可循的工程实践。
本章将围绕三大维度——结构高效(模型表示)、数值高效(精度优化)、架构高效(硬件实现)——建立系统的理论与实践框架。我们将剖析量化如何实现内存压缩与推理加速,剪枝如何在保精度的前提下消除参数冗余,知识蒸馏如何将复杂模型能力迁移到高效结构。最终目标不仅仅是提升单一性能指标,而是让复杂 AI 能力在各种计算环境和应用领域都能高效落地。
优化框架
优化过程贯穿三大维度,连接了软件算法与硬件执行,如下图所示。理解这些维度及其关系,是掌握本章所有技术的基础。

本章将以工程视角,逐层讲解量化(训练后量化与感知量化)、剪枝(基于幅值、结构化、动态剪枝)、蒸馏(温度缩放、特征迁移)等具体算法,并探讨它们如何协同作用,以及其效果如何受目标硬件特性影响。该框架为系统性优化决策提供指导,确保模型变换既满足部署约束,又保留核心能力。
本章将前述高效性理念转化为可操作的工程实践,通过系统性应用优化原理,让工程师掌握量化、剪枝、蒸馏等核心工具,实现复杂模型在多样计算环境下的高效部署。优化框架有效弥合了理论模型能力与实际部署需求之间的鸿沟,使机器学习系统在真实场景中兼具性能与效率。
部署场景
机器学习模型总是作为更大系统的一部分运行,面临复杂的约束、依赖与权衡。模型优化绝非纯粹的算法问题,而是系统级挑战,需兼顾计算效率、可扩展性、部署可行性与整体系统性能。可参考 第 13 章:机器学习运维 的运维原则,理解模型优化的系统视角、优化动因、关键约束与有效策略的本质。
实际部署
现代机器学习模型在基准数据集上精度惊人,但让其在真实场景中可用却极具挑战。无论云端、手机还是微控制器,机器学习系统都受限于计算、内存、延迟和能耗,这些约束极大影响训练与推理。研究环境下表现优异的模型,集成到实际系统后往往难以落地。
此外,现实可行性不仅仅是精度,还包括训练、存储、执行等多方面的效率。1
不同部署场景对效率的要求各异。云端大规模 ML 需优化模型以缩短训练时间、降低算力和能耗成本。边缘 ML2 则要求模型在极有限的算力下运行,需极致压缩内存和计算复杂度。移动端还需兼顾电池寿命与实时响应,而 Tiny ML3 则追求极致能效,模型需适配超低功耗设备的极小内存和算力。
优化还助力可持续与普惠 AI,具体可参考 第 18 章:可持续 AI 。随着 AI 规模化,降低模型能耗有助于减缓大规模训练与推理的环境影响。优化后的模型还能拓展 AI 的应用边界,支持低资源环境下的医疗、野外自主系统等场景。
权衡平衡
精度与效率的矛盾是所有优化决策的核心。提升模型容量通常能增强预测性能,但也会带来更高的计算成本,导致推理变慢、资源消耗增加。这种提升还会带来内存占用4、推理延迟、能耗、训练效率等多方面的挑战。随着模型部署到多样硬件平台,如何平衡精度与效率成为模型优化的关键。
这种矛盾在不同部署场景下表现各异。训练阶段算力需求随模型规模线性增长,推理阶段则需严格控制延迟与能耗,尤其在实时应用中。
框架应用与导航
本节提供将优化技术应用于实际问题的指导,说明系统约束如何映射到优化维度,并给出技术选择的导航策略。
约束映射
理解系统约束与优化维度的映射,有助于在面对部署难题时快速定位最相关的优化方向。内存带宽受限时,应优先考虑模型结构与数值精度优化;延迟瓶颈则需关注模型结构与架构效率。
下表总结了不同系统约束与三大优化维度的对应关系。
| 系统约束 | 模型结构 | 数值精度 | 架构效率 |
|---|---|---|---|
| 计算成本 | ✗ | ✓ | ✓ |
| 内存与存储 | ✓ | ✓ | ✗ |
| 延迟与吞吐 | ✓ | ✗ | ✓ |
| 能效 | ✗ | ✓ | ✓ |
| 可扩展性 | ✓ | ✗ | ✓ |
这种系统化映射,继承了 第 9 章:高效 AI 中提出的高效性原则。此处聚焦于模型级优化,通过具体技术实现这些原则。虽然每种约束主要对应某一优化维度,但实际关系并非一一对应,许多技术会同时影响多个约束。以三维结构梳理优化技术,有助于更有效地分析权衡,选择最契合部署需求的优化方案。
技术导航
本章涵盖了模型结构、数值精度、架构效率三大维度的优化技术工具箱。但并非所有技术都适用于每个问题,技术种类繁多也容易让人无从下手。以下导航建议可帮助你根据实际约束和目标快速定位切入点。
如上表所示,内存或模型体积受限时,应优先考虑模型结构和数值精度优化(如参数裁剪、低比特量化);推理延迟受限时,则应关注模型结构和架构效率(如减少计算量、提升硬件利用率);训练或推理成本受限时,优先考虑数值精度和架构效率(如混合精度、算子融合);若精度损失不可接受,则需采用训练感知型优化(如感知量化、剪枝后微调),而非简单的训练后处理。
生产系统通常遵循成熟模式:快速部署时采用训练后量化等方法,几小时内实现 4-8 倍压缩,精度损失 1-2%;生产级优化则多步组合(先裁剪参数,再微调恢复精度,最后量化),可达 8-15 倍压缩,精度损失 <1%,周期数周;极端约束(如 <1MB TinyML)则需从架构设计阶段引入自动化搜索与超低精度,周期数月。
模型优化本质是系统工程问题,效果高度依赖目标硬件:同样的量化技术,在专用加速器上可达 4 倍加速,在通用处理器上仅 1.5 倍。不同模型结构和任务对优化的容忍度也不同,如视觉模型通常比语言模型更易压缩。优化需反复测量、迭代调整,而非“一步到位”。若系统瓶颈在数据预处理或网络 IO,模型优化收益有限,因此优化前务必进行系统级性能分析(详见后续“策略与实施”章节)。
本章内容支持非线性阅读。工程师可聚焦数值精度部分的训练后技术,快速提升现有模型效率;研究者和进阶读者需深入理解数学原理与集成方法;初学者可按章节递进,从基础到进阶,逐步掌握优化全貌。
优化三维
每个优化维度都值得深入探讨。如图所示,模型结构优化决定“做什么计算”,数值精度优化决定“如何计算”,架构效率优化则确保“计算能高效运行在目标硬件上”。
模型结构
第一维“模型结构优化”聚焦于消除神经网络中的冗余。大模型往往包含大量对性能贡献有限的参数,导致内存和计算成本大幅增加。结构优化通过剪枝、知识蒸馏、自动架构搜索等方法,去除无用部分,兼顾效率与精度。这些优化主要作用于算法层面,确保模型既有效又可控。
数值精度
结构优化决定“做什么”,精度优化则决定“怎么做”。本节关注权重、激活、算术运算的数值表示与处理方式。量化技术将高精度权重和激活映射为低比特表示,使模型能高效运行在 GPU、TPU、AI 专用芯片等硬件上(详见 第 11 章:AI 加速 )。混合精度训练5则在训练过程中动态调整精度,实现效率与精度的平衡。
合理的数值精度优化能大幅降低计算成本,同时保持可接受的精度,让复杂模型在资源受限环境下可用。
架构效率
第三维“架构效率”关注训练与推理阶段的高效计算。即使模型结构设计合理,若执行效率低下,整体性能仍然受限。许多模型的计算图存在冗余,导致算子调度与执行效率低。稀疏性6是提升架构效率的关键技术,通过利用零值参数减少计算量。
架构效率还包括稀疏权重与激活的利用、大型算子分解7、基于输入复杂度的动态计算等。
这些方法提升了不同硬件平台上的执行效率,降低延迟与能耗。相关理念也适用于训练,如梯度检查点、低秩适配8等技术可降低训练内存和计算需求。
三维优化框架
三维框架的交互性体现在技术协同上。剪枝主要作用于结构,但也影响架构效率(减少推理计算);量化聚焦数值精度,同时影响内存和执行效率。理解这些相互作用,有助于实现最优的优化组合。
这种交互性意味着,优化选择受系统约束驱动。数据中心与移动端、嵌入式系统的约束完全不同。计算成本、内存、延迟、能效等因素共同决定最适合的优化方案。资源极度受限时需激进剪枝与量化,延迟敏感场景则需算子融合9与硬件感知调度。
如上表所示,约束与优化策略之间存在多对多关系,许多技术会同时影响多个约束。
接下来将系统梳理每一维度,首先从模型结构优化(即通过调整神经网络结构和参数消除冗余)展开。
结构化模型优化方法
模型结构优化通过调整神经网络结构和参数,在保证精度的前提下提升效率。现代模型往往为追求精度而牺牲效率,参数冗余导致成本高、推理慢。结构优化的目标有二:一是消除冗余(利用过参数化,模型可用更少参数实现相近性能),二是通过梯度检查点10、并行计算11等技术为高效硬件执行重构计算。
优化的难点在于权衡多重约束12。过度压缩会导致精度大幅下降,优化不足则模型过大、过慢,难以部署。选择合适技术需理解模型体积、计算复杂度、泛化性能之间的权衡。
三大核心技术应对这一挑战:剪枝消除低影响参数,知识蒸馏迁移能力到小模型,NAS 自动化设计满足特定约束。三者可组合使用,协同提升优化效果。
剪枝
内存墙成为系统性能瓶颈:模型越大,内存带宽越成限制。剪枝正面应对这一约束,通过参数裁剪降低内存需求。最前沿模型常含数百万乃至数十亿参数,其中许多对预测贡献极小。大模型虽提升表达力和泛化,但也带来内存、计算、可扩展性等多重低效,影响云、边缘、移动等多场景的训练与部署。
保持精度所需的参数远少于模型总参数。许多权重对决策影响极小,可在不损失性能的前提下移除,实现效率提升。这种冗余源于现代神经网络的过参数化,训练时有助于优化,但部署时为压缩提供了空间。模型压缩可参考 第 3 章:深度学习基础 ,过参数化为压缩创造了理论基础。剪枝正是系统性移除冗余参数、保留精度的优化技术。
剪枝定义
剪枝 是一种 模型优化技术,通过移除神经网络中 不必要的参数,在保持 预测性能 的前提下,减少 模型体积与计算成本,提升 存储、推理与部署效率。剪枝让模型在无需重构架构的情况下变得更小、更快、更高效,直接应对机器学习系统的内存、计算、可扩展性约束,是多硬件平台部署的关键技术。
主流框架已内置剪枝 API,如 PyTorch 的 torch.nn.utils.prune,TensorFlow 的 Model Optimization Toolkit13 提供 tfmot.sparsity.keras.prune_low_magnitude() 等函数,将复杂算法转化为易用接口,极大降低了优化门槛。
剪枝示例
剪枝的核心思想是识别对预测影响最小的权重并移除,保持精度的同时提升稀疏性。最直观的方法是基于权重幅值,绝对值小的权重通常对输出影响小,可优先裁剪。
下例展示了对 3×3 权重矩阵的幅值剪枝,简单阈值即可实现稀疏化。
import torch
import torch.nn.utils.prune as prune
# 原始稠密权重矩阵
weights = torch.tensor(
[[0.8, 0.1, -0.7], [0.05, -0.9, 0.03], [-0.6, 0.02, 0.4]]
)
# 幅值剪枝:移除绝对值 < 0.1 的权重
threshold = 0.1
mask = torch.abs(weights) >= threshold
pruned_weights = weights * mask
print("Original:", weights)
print("Pruned:", pruned_weights)
# 结果:9 个权重仅保留 4 个(稀疏度 44%)
该例体现了剪枝的本质:在保证性能的前提下最小化参数量。我们将非零参数从 9 降至 4($k=4$),幅值最小的权重(0.1、0.05、0.03、0.02)被移除,较大权重(0.8、-0.9、-0.7、-0.6、0.4)被保留。
将这一思路扩展到完整神经网络时,需同时考虑裁剪比例(稀疏度)与选择标准。下图展示了在更大权重矩阵上的应用。
如图所示,剪枝通过移除小幅值权重,将稠密矩阵转化为稀疏表示,显式实现了 $\ell_0$-范数约束。

数学表述
剪枝的目标可简述为:在最小化预测误差的前提下,找到非零权重最少(体积最小)的模型。该目标可形式化为如下优化问题:
$$ \min_{\hat{W}} \mathcal{L}(\hat{W}) \quad \text{subject to} \quad |\hat{W}|_0 \leq k $$
其中 $\mathcal{L}(\hat{W})$ 为剪枝后模型的损失函数,$\hat{W}$ 为剪枝后参数,$|\hat{W}|_0$ 表示 L0-范数(非零参数个数),$k$ 为参数预算。
L0-范数直接衡量模型体积,决定内存和计算成本。但 L0-范数最小化是 NP-hard 问题,实际算法多用幅值、梯度、二阶敏感度等启发式近似。
在上例中,$|\hat{W}|_0$ 从 9 降至 4($k=4$),幅值阈值即为选择标准。L1/L2 范数虽能鼓励权重变小,但不能保证严格为零,需显式阈值化才能真正减少内存和计算。
为提升可行性,实际方法常将硬约束转为软正则项: $$ \min_W \mathcal{L}(W) + \lambda | W |_1 $$ $\lambda$ 控制稀疏度,L1-范数鼓励权重变小但不强制为零。也有迭代启发式方法,每轮移除最小幅值参数并微调恢复精度。
剪枝结构
剪枝可针对神经网络的不同结构,主要包括神经元、通道、层,每种方式对架构和性能影响各异。
- 神经元剪枝:移除整个神经元及其相关权重和偏置,常用于全连接层,减少层宽。
- 通道剪枝(或滤波器剪枝):常用于卷积网络,移除整个通道或滤波器,减少特征图深度,适合对计算效率要求高的图像任务。
- 层剪枝:移除整个层,显著减少网络深度,但需谨慎平衡模型容量。
下图展示了通道剪枝与层剪枝的区别。通道剪枝需调整后续层的输入通道数,层剪枝则需重连剩余层。无论哪种方式,微调都是恢复性能的关键。

非结构化剪枝
非结构化剪枝移除单个权重,保持网络结构不变。训练过程中部分连接变得冗余,移除这些弱连接可降低内存需求,精度影响有限。
数学上,非结构化剪枝通过对权重矩阵 $W \in \mathbb{R}^{m \times n}$ 应用二值掩码 $M \in {0,1}^{m \times n}$,得到稀疏权重矩阵: $$ \hat{W} = M \odot W $$ $\odot$ 为 Hadamard 乘积。掩码 $M$ 通常基于幅值阈值生成,移除幅值最小的 $s$ 部分权重。阈值 $\tau$ 满足: $$ M_{i,j} = \begin{cases} 1, & \text{if } |W_{i,j}| > \tau \ 0, & \text{otherwise} \end{cases} $$ $\tau$ 保证仅保留最大 $(1-s)$ 部分权重。
非结构化剪枝的优势在于内存效率,适合嵌入式、移动端等内存受限场景。但在主流硬件(GPU/TPU)上,稀疏矩阵难以充分利用加速器,需专用稀疏计算内核。因此,非结构化剪枝主要提升存储效率,对推理加速有限。
结构化剪枝
结构化剪枝14移除整个神经元、滤波器、通道或层,生成更小的稠密模型,适合硬件加速。与非结构化剪枝相比,结构化剪枝直接减少网络规模,推理加速效果更明显。
结构化剪枝的核心在于识别对预测贡献小的结构单元。常用方法包括:
- 幅值剪枝:按权重范数(L1/L2)移除权重较小的神经元/滤波器,简单高效。
- 激活剪枝:统计神经元/滤波器在数据集上的平均激活值,低激活单元可移除,需额外数据分析。
- 梯度剪枝:利用训练过程中的梯度信息,移除对损失影响小的单元,通常在训练阶段应用。
下图对比了非结构化与结构化剪枝。左侧为非结构化剪枝(随机移除连接,形成稀疏矩阵),需专用内核。中间和右侧为结构化剪枝(移除神经元/滤波器,结构更规整),适合硬件加速。

不同方法在计算复杂度和效果上各有权衡。幅值剪枝简单高效,但不考虑数据分布;激活剪枝更数据驱动,但需额外计算;梯度剪枝利用训练动态,适合大模型但实现复杂。具体选择需结合部署环境和性能需求。
动态剪枝
传统剪枝(无论结构化还是非结构化)多为静态剪枝,即训练后或训练中定期移除参数,假设参数重要性固定。但实际中,参数重要性可能随输入或训练动态变化。动态剪枝则根据输入或训练过程实时调整剪枝决策。
动态剪枝可通过运行时稀疏性实现,如激活条件剪枝:对特定输入,动态关闭激活值低的神经元/通道,实现输入相关的稀疏模式,推理时按需分配计算资源,提升效率。
如卷积网络处理不同复杂度图片,简单图片许多滤波器激活值极低,动态剪枝可临时跳过这些计算,提升效率且不损失精度。该方法特别适合延迟敏感场景,与 第 12 章:AI 基准测试 中的性能测量策略相关。
另一类动态剪枝在训练阶段逐步引入稀疏性,如渐进幅值剪枝,先用稠密网络训练,逐步提升剪枝比例,每轮微调恢复精度。与静态剪枝不同,动态剪枝允许网络在后期恢复部分被剪参数,提升灵活性。
动态剪枝优点在于可适应不同工作负载,兼顾效率与精度,避免过度剪枝。但实现复杂度高,需实时决策,适合边缘计算、自适应 AI 系统(详见 第 14 章:设备端学习 ),对生产部署和监控提出更高要求(见 第 13 章:机器学习运维 )。
剪枝权衡
不同剪枝技术在内存效率、计算效率、精度保持、硬件兼容性、实现复杂度等方面各有权衡。具体选择需结合系统约束和部署环境,参考 第 13 章:机器学习运维 的运维实践。
非结构化剪枝适合模型压缩、内存受限场景,但对推理加速有限。结构化剪枝直接减少 FLOPs,适合实时推理、移动/边缘 AI、高效训练,但对精度影响更大,需微调恢复。动态剪枝则在效率与精度间动态平衡,但实现复杂度高。
下表总结了三类剪枝方式的结构差异及对模型和执行的影响。
| 方面 | 非结构化剪枝 | 结构化剪枝 | 动态剪枝 |
|---|---|---|---|
| 移除内容 | 单个权重 | 整个神经元、通道、滤波器或层 | 运行时动态调整 |
| 模型结构 | 稀疏权重矩阵,结构不变 | 架构被修改,剪枝层完全移除 | 结构可动态变化 |
| 内存影响 | 通过移除非零权重降低存储 | 通过移除结构单元降低存储 | 取决于实时剪枝 |
| 计算影响 | 需专用稀疏计算,否则加速有限 | 直接减少 FLOPs,加速推理 | 动态平衡精度与效率 |
| 硬件兼容性 | 需专用稀疏计算支持 | 适合主流深度学习硬件 | 需自适应推理引擎 |
| 需微调? | 剪枝后常需微调恢复精度 | 结构变化大,更需微调 | 动态调整,微调需求低 |
| 典型场景 | 云端模型压缩、内存优化 | 实时推理、移动/边缘 AI、高效训练 | 自适应 AI、实时系统 |
剪枝策略
除上述三大类,剪枝流程也影响效率与精度。常见有迭代剪枝与一次性剪枝,各有优劣。
迭代剪枝
迭代剪枝采用多轮“剪枝 - 微调”循环,每轮移除少量结构单元,微调恢复性能。这样可避免精度骤降,让网络逐步适应复杂度降低。
如图所示,假设需从卷积网络中剪除 6 个通道,迭代剪枝每轮移除 2 个,分三轮完成。每轮后微调恢复精度。第一轮剪枝后精度从 0.995 降至 0.971,微调后恢复至 0.992。三轮后最终精度为 0.991,仅比原始模型低 0.4%,通道数减少 27%。分步调整让网络在压缩的同时保持性能。

一次性剪枝
一次性剪枝则在单步移除多个结构单元,随后进行长时间微调。该方法压缩速度快,但精度损失大,网络难以适应剧烈结构变化。
如图所示,同样移除 6 个通道,一次性剪枝直接全部移除,精度从 0.995 降至 0.914,微调后仅恢复到 0.943,精度下降 5%。与迭代剪枝相比,性能损失更大。

剪枝策略选择需综合考虑参数压缩目标、计算资源、性能需求、开发周期、目标平台等因素。高压缩目标建议迭代剪枝,资源有限或对精度要求不高可用一次性剪枝。生产环境多采用迭代剪枝以最大限度保留性能。
彩票假说
剪枝不仅仅是压缩模型,最新研究发现,剪枝还能揭示原始大模型中本就存在的高效子网络,这就是“彩票假说”15(Lottery Ticket Hypothesis,LTH)。
LTH 通过迭代剪枝发现:大模型训练收敛后,移除幅值最小权重,剩余权重重置为原始值而非重新随机化,重复多轮,最终得到的“中奖子网”可单独训练,精度与全模型相当甚至更优。

LTH 的意义在于:未来或许无需先训练大模型再剪枝,而是直接训练高效子网,彻底改变模型训练范式。LTH 也强调了初始化的重要性,中奖子网只有在原始初始化下才能保留性能。该理论进一步证明了迭代剪枝优于一次性剪枝。
但实际应用 LTH 仍需大量剪枝 - 重训练循环,计算成本高。当前研究正探索能否在训练早期直接识别中奖子网,若能实现,将彻底重塑模型训练与优化流程。
虽然 LTH 主要是理论突破,实际部署仍依赖主流框架的结构化与非结构化剪枝工具。
剪枝实践
许多主流机器学习框架都内置了结构化和非结构化剪枝工具,支持剪枝后模型的微调,并针对云端、边缘和移动端部署进行优化。
如 PyTorch、TensorFlow 和 ONNX 等机器学习框架,均提供专用的剪枝工具,帮助开发者高效实现剪枝,并确保与目标硬件的兼容性。
在 PyTorch 中,剪枝功能通过 torch.nn.utils.prune 模块实现,支持对单层或整个模型进行基于权重幅值的剪枝。用户可以通过设置阈值,将幅值最小的一部分权重置零(非结构化剪枝),或直接移除整个神经元或卷积核(结构化剪枝)。PyTorch 还允许自定义剪枝策略,例如基于激活值或梯度的剪枝。剪枝完成后,通常需要对模型进行微调,以恢复精度,然后导出用于推理。
TensorFlow 通过 Model Optimization Toolkit(TF-MOT)提供剪枝支持。该工具包将剪枝过程直接集成到训练流程中,通过稀疏性正则化动态选择待移除的参数。TensorFlow 剪枝 API 支持全局和分层剪枝,通常在训练阶段应用,使模型从一开始就学习稀疏结构,而非训练后再剪枝。TF-MOT 还支持将剪枝后的模型导出为 TFLite 格式,便于在移动和边缘设备上部署。
ONNX16 作为开放的模型表示标准,本身不直接实现剪枝,但支持从 PyTorch、TensorFlow 等框架导出的剪枝模型。ONNX 设计为硬件无关,便于将剪枝后的模型进一步优化为适配 TensorRT17、OpenVINO、EdgeTPU 等推理引擎。这些推理引擎可进一步利用结构化和动态剪枝,在专用硬件加速器上提升执行效率。
尽管框架层面对剪枝的支持日益完善,实际应用时仍需充分考虑硬件兼容性和软件优化。标准 CPU 和 GPU 通常不直接加速稀疏矩阵运算,因此非结构化剪枝虽能降低内存占用,但对计算速度提升有限。相比之下,结构化剪枝更易被推理引擎支持,能直接减少推理时的计算量。动态剪枝若与推理引擎深度集成,可根据负载和硬件约束自适应优化执行,特别适用于自适应 AI 应用场景。
在实际工程中,剪枝策略的选择需权衡内存效率、计算性能、精度保持和实现复杂度等多方面因素。这些权衡决定了剪枝方法在真实机器学习工作流中的应用方式,并影响部署方案的资源和系统需求。
为帮助决策,@tbl-pruning-tradeoffs(注:请替换为标准表格引用)总结了各类剪枝方法在效率与易用性方面的主要对比,便于开发者根据实际需求选择合适的剪枝策略。
这些权衡强调了剪枝方法需与实际部署需求紧密结合。PyTorch、TensorFlow、ONNX 等框架为开发者提供了丰富的实现手段,但剪枝效果最终取决于底层硬件和具体应用场景。
| 指标 | 非结构化剪枝 | 结构化剪枝 | 动态剪枝 |
|---|---|---|---|
| 内存效率 | ↑↑ 高 | ↑ 中等 | ↑ 中等 |
| 计算效率 | → 中性 | ↑↑ 高 | ↑ 高 |
| 精度保持 | ↑ 中等 | ↓↓ 低 | ↑↑ 高 |
| 硬件兼容性 | ↓ 低 | ↑↑ 高 | → 中性 |
| 实现复杂度 | → 中性 | ↑ 中等 | ↓↓ 高 |
例如,结构化剪枝因其对主流推理引擎的良好兼容性,常用于移动和边缘端应用;而动态剪枝则更适合需要实时调整稀疏度的自适应 AI 工作负载。非结构化剪枝虽能极大降低内存占用,但若无专用稀疏计算内核,难以获得显著的计算加速。
理解这些权衡对于实际部署剪枝模型至关重要。许多知名模型已成功集成剪枝以优化性能。例如,MobileNet 作为轻量级卷积神经网络,通过剪枝降低推理延迟且保持精度。BERT18 这类主流 NLP 模型,通过剪枝注意力头和中间层,衍生出 DistilBERT19、TinyBERT 等高效版本,在大幅减少计算量的同时保留了大部分性能。在计算机视觉领域,EfficientNet20 通过剪枝冗余卷积核,优化了在资源受限环境下的部署表现。
知识蒸馏
想象一位世界级教授(教师模型),博览群书、理解深刻;而一位聪明的学生(学生模型)需要快速掌握知识。教授不仅给出标准答案(硬标签),还会详细解释每个选项的优劣及其内在联系(软标签)。学生通过这种丰富的指导,比单靠课本学得更好。这正是知识蒸馏的本质。
知识蒸馏通过让小型学生模型在训练时借助大型教师模型的指导,学习教师输出的概率分布(软标签),而非仅依赖正确/错误的硬标签。教师模型输出的概率分布比真实标签更丰富。例如,图像分类中,真实标签可能是“狗”(one-hot:[0, 1, 0, 0, …]),而教师模型输出可能为 [0.02, 0.85, 0.08, 0.05, …],表明“狗”最可能,但“狼”“狐狸”也有一定相似性。这种类别间的相似性信息有助于学生模型学习特征关系,是硬标签无法传递的。
知识蒸馏与剪枝不同。剪枝是在已有模型上移除参数,而蒸馏则是用教师模型指导训练一个独立的小模型。学生模型优化目标是拟合教师的软预测分布(类别概率分布),而不仅仅是拟合标签。
下图(图 8)展示了蒸馏流程。教师模型通过带温度参数 $T$ 的 softmax 生成概率分布,学生模型同时利用软目标和真实标签进行训练。

学生模型训练包含两个损失项:
- 蒸馏损失:通常基于 Kullback-Leibler (KL) 散度21,最小化学生与教师软标签分布的差异。
- 学生损失:标准交叉熵损失,确保学生模型能正确分类硬标签。
两者结合,使学生模型既能吸收教师的结构化知识,又能获得数据集的标签监督。这样,小模型也能接近大模型的精度,是模型压缩和高效部署的关键技术。
知识蒸馏让小模型达到常规训练难以企及的精度,尤其适用于实时推理、云到端模型压缩、低功耗 AI 等场景。
蒸馏理论
知识蒸馏的理论基础在于,训练良好的教师模型蕴含了远超正确类别标签的信息。传统监督学习仅最小化预测与真实标签的交叉熵损失22,只提供每类的硬决策边界,忽略了模型对类别间关系的理解。
知识蒸馏通过教师模型输出的软概率分布,传递了更多信息。学生模型不仅要拟合正确标签,还要拟合教师对所有类别的概率分布。为此,引入温度缩放 softmax,使概率分布更平滑,便于学生学习。
蒸馏数学原理
温度机制的数学表达如下,设 $z_i$ 为第 $i$ 类的 logits,标准 softmax 计算概率为: $$ p_i = \frac{\exp(z_i)}{\sum_j \exp(z_j)} $$
知识蒸馏中引入温度参数23 $T$,softmax 变为: $$ p_i(T) = \frac{\exp(z_i / T)}{\sum_j \exp(z_j / T)} $$ 温度越高,概率分布越平滑,揭示模型对不同类别的不确定性。
学生模型的损失函数通常为: $$ \mathcal{L}{\text{distill}} = (1 - \alpha) \mathcal{L}{\text{CE}}(y_s, y) + \alpha T^2 \sum_i p_i^T \log p_{i, s}^T $$ 其中:
- $\mathcal{L}_{\text{CE}}(y_s, y)$ 为学生预测与真实标签的交叉熵损失;
- 第二项为教师与学生软预测分布的 KL 散度;
- $T^2$ 保证高温度下梯度合适;
- $\alpha$ 控制两项损失的权重。
通过同时学习硬标签和教师软输出,学生模型能继承教师的泛化能力,即使参数更少,也能区分相似类别。
蒸馏直观理解
通过结合硬标签和软输出,学生模型不仅学会了正确答案,还能理解类别间的相对关系。举例来说,图像分类任务中,硬标签只告诉模型“猫”是正确答案,“狗”“狐狸”都错;而教师模型的软输出会显示“猫”最可能,“狗”也有一定概率,“狐狸”则很低。如下图(图 9)所示,软目标分布反映了模型对不同类别的相对信心。

教师模型的这种细腻信号,帮助学生模型建立更合理的决策边界,提升对真实世界模糊数据的稳健性。
当训练数据有限或噪声较大时,蒸馏尤为有效。大模型在大数据集上训练,已具备良好泛化能力,学生模型通过蒸馏继承这些能力,相当于间接获得了更丰富的训练信号。
知识蒸馏还具有正则化作用。软目标将概率分布在多个类别上,防止学生模型过拟合硬标签,提高泛化能力,降低对抗样本敏感性。尤其是小模型更易过拟合,蒸馏能显著提升其泛化性能。
此外,蒸馏有助于将大模型压缩为小型高效版本,支持 第 18 章:可持续 AI 的绿色部署目标。直接训练小模型往往精度较低,而借助教师模型,学生模型能达到更高精度,非常适合边缘计算、移动端等资源受限场景(详见 第 14 章:设备端学习 )。
效率提升
知识蒸馏在内存效率、计算效率和部署灵活性三方面均有显著优势。与剪枝不同,蒸馏从头训练紧凑模型,借助教师指导获得常规训练难以达到的精度,支持 第 12 章:AI 基准测试 的结构化评测。
内存与模型压缩
蒸馏的核心优势在于,小模型能保留大部分预测能力,显著降低内存占用。这对移动端、嵌入式 AI 等资源受限环境尤为重要,模型体积直接影响存储和加载速度。
如 NLP 领域的 DistilBERT、CV 领域的 MobileNet 蒸馏版,均能以一半参数保留 97% 的大模型精度,优于激进剪枝带来的性能损失。
蒸馏还能将教师模型的稳健性和泛化能力传递给学生。大模型通常在大数据集上训练,泛化能力强,学生模型继承后更不易过拟合,适应多样化部署环境。对于小数据场景,蒸馏尤为有效。
计算与推理加速
学生模型通过紧凑结构近似教师知识,推理所需 FLOPs 更少,执行更快。与非结构化剪枝不同,蒸馏后模型仍为稠密结构,兼容主流 AI 加速器(GPU、TPU、边缘芯片)。
实际部署中,这意味着:
- 推理延迟降低,适合实时 AI 应用(如语音识别、推荐系统、自动驾驶感知等);
- 能耗更低,适合移动和 IoT 场景;
- 云端推理吞吐量提升,支持大规模 AI 服务以更低算力维持模型质量。
例如,NLP 领域的 Transformer 模型常用蒸馏技术,将推理延迟降低 2-4 倍,便于大规模在线服务。
部署与系统考量
知识蒸馏也适用于多任务学习场景。一个大型教师模型可指导多个学生模型,分别适配不同任务或语言,无需从头训练。CV 领域中,教师模型可为人脸识别、医学影像、自动驾驶等专用学生模型蒸馏知识。
蒸馏后的学生模型还可结合剪枝、量化、图优化等进一步加速,确保在多种硬件环境下高效推理,尤其适合边缘和移动端部署。
但蒸馏也有局限性。其效果依赖教师模型质量,若教师训练不充分,可能传递错误偏差。蒸馏需额外训练阶段,增加训练成本。设计合适的学生模型结构也有挑战,过小的学生模型难以完全吸收教师知识。
权衡分析
与剪枝相比,知识蒸馏更能保持精度,但训练复杂度更高(需训练师生两套模型)。剪枝则直接带来计算效率提升,尤其是结构化剪枝。实际工程中,常将剪枝与蒸馏结合,如 DistilBERT、MobileBERT 先剪枝再蒸馏,取得最佳权衡。下表总结了两者的主要权衡。
| 指标 | 知识蒸馏 | 剪枝 |
|---|---|---|
| 精度保持 | 高——学生从教师学习,泛化能力强 | 变化大——过度剪枝易损失精度 |
| 训练成本 | 高——需训练教师和学生 | 低——仅需微调 |
| 推理速度 | 高——生成稠密、优化模型 | 取决于剪枝类型——结构化高效,非结构化需专用支持 |
| 硬件兼容性 | 高——兼容主流加速器 | 有限——稀疏模型需专用执行 |
| 实现难度 | 复杂——需设计师生训练流程 | 简单——训练后直接应用 |
知识蒸馏是 ML 系统优化的重要技术,常与剪枝、量化等结合用于生产部署。理解蒸馏与其他优化手段的协同关系,是构建高效多阶段优化流水线的关键。
结构化近似
基于近似的压缩技术通过重构模型参数表示,降低复杂度同时保持表达能力,是对剪枝和蒸馏的有力补充。
与剪枝直接移除参数、蒸馏迁移知识不同,结构化近似方法通过分解大规模权重矩阵或张量为低维组件,实现高效存储与计算。这类方法基于高维表示可用低秩结构良好近似的观察,显著减少参数数量且性能损失有限。常见方法包括:
- 低秩矩阵分解(LRMF):将权重矩阵分解为低秩矩阵乘积,降低存储和计算复杂度。
- 张量分解:将高维张量分解为低秩组件,适用于多路交互的神经网络结构。
这些方法在边缘 ML、Tiny ML 等资源受限场景下尤为有效。低秩分解和张量分解通过减少运算量,加速模型训练与推理。下文将详细介绍低秩矩阵分解与张量分解的数学基础、应用及权衡。
低秩分解
许多机器学习模型的权重矩阵存在大量冗余,导致计算、存储和部署效率低下。前文介绍的剪枝和蒸馏,分别通过移除参数和知识迁移来压缩模型,但并未改变参数结构。低秩矩阵分解(LRMF)则通过将大矩阵近似为低秩乘积,从结构上实现紧凑表达,无需显式移除或迁移信息。
这种结构化压缩在边缘计算、云推理、硬件加速等场景下尤为重要。通过低秩近似,模型在保持大部分信息的同时,显著减少参数存储和计算量,是优化机器学习架构的有力工具。
训练数学原理
LRMF 是线性代数和机器学习中的经典技术,用于将高维矩阵分解为低维矩阵乘积,从而实现更紧凑的参数表示,降低内存和计算复杂度,同时保留重要结构信息。其数学表达为:
给定 $A \in \mathbb{R}^{m \times n}$,LRMF 寻找 $U \in \mathbb{R}^{m \times k}$、$V \in \mathbb{R}^{k \times n}$,使得: $$ A \approx UV $$ 其中 $k$ 为近似秩,远小于 $m, n$。常用奇异值分解(SVD)实现: $$ A = U \Sigma V^T $$ $\Sigma$ 为奇异值对角阵,$U, V$ 为正交矩阵。保留前 $k$ 个奇异值即可得到低秩近似。
下图(图 10)展示了低秩分解带来的参数量减少。原始矩阵 $M$ 可近似为 $L_k$ 与 $R_k^T$ 的乘积。以全连接层为例,原本需存储 $m \times n$ 参数,分解后仅需 $m \times k + k \times n$,只要 $k < n/2$,总参数量更少,计算复杂度为 $O(mkn)$。

LRMF 广泛用于提升机器学习模型效率,尤其适合全连接层和卷积层。通过分解,模型推理速度、存储效率和硬件适应性均有提升。
全连接层权重矩阵大,最适合分解。原本需存储 $m \times n$,分解后仅需 $m \times k + k \times n$,极大降低存储和计算量,适合云到端 ML 流水线。
卷积层也可通过分解卷积核为可分离结构(如深度可分离卷积)实现高效计算,与现代 AI 加速器的硬件优化高度契合。
在推荐系统等协同过滤场景,LRMF 可分解用户 - 物品交互矩阵,提取用户偏好和物品属性的潜在因子,实现高效推荐。
分解效率与挑战
分解后,参数量从 $O(mn)$ 降至 $O(mk + kn)$,但推理需额外一次矩阵乘法,可能增加延迟。实际工程中需权衡存储与实时推理速度。
秩 $k$ 的选择是 LRMF 的关键。$k$ 越小压缩越强但信息损失大,$k$ 越大保留信息多但压缩有限。实际常用交叉验证或启发式方法确定最优秩。
实际数据常含噪声或缺失值,影响分解质量。可通过 $L_2$ 正则等方法提升稳健性,确保分解在不同系统架构下表现稳定。
低秩分解为模型压缩提供了高效路径,尤其适合边缘计算等资源受限场景。尽管面临秩选择和计算开销等挑战,LRMF 仍是 ML 系统设计与部署的重要优化工具。
张量分解
现代神经网络常用多维张量而非二维矩阵,如卷积层、注意力机制、嵌入层等。此时,标准矩阵分解难以高效表达多路交互,需采用更通用的张量分解技术。

张量分解(TD)将低秩分解原理推广到高阶张量,能将大规模多维数组表达为低秩因子之和(见 图 11)。张量在 ML 系统中广泛用于权重、激活、输入特征等表示,直接存储和计算代价高昂,需高效分解。
张量分解常用方法包括:
CP 分解:将张量表示为若干秩一张量之和。对 $\mathcal{A} \in \mathbb{R}^{m \times n \times p}$,有 $$ \mathcal{A} \approx \sum_{r=1}^{k} u_r \otimes v_r \otimes w_r $$ 其中 $u_r, v_r, w_r$ 为因子向量,$k$ 为秩。
Tucker 分解:引入核心张量 $\mathcal{G}$ 和因子矩阵 $U, V, W$,有 $$ \mathcal{A} \approx \mathcal{G} \times_1 U \times_2 V \times_3 W $$ $\times_i$ 表示第 $i$ 维张量 - 矩阵乘法。
Tensor-Train (TT) 分解:将高阶张量分解为一系列低秩张量核,极大降低存储和计算复杂度。
这些分解方法在 ML 系统中用于降低参数冗余,同时保持表达能力。下节将介绍其在模型结构中的应用及计算权衡。
张量分解应用
张量分解广泛用于提升 ML 系统的效率和可扩展性。通过分解高维张量为低秩表示,既降低了内存和计算需求,又保留了模型表达能力。典型应用包括:
- CNN:分解卷积核,减少推理运算量,适合边缘和移动端部署。
- NLP:分解嵌入层和注意力机制,降低存储和推理成本。
- 硬件加速:分解优化数据流和并行计算,提升 AI 芯片利用率。
但张量分解也带来秩选择、分解计算开销等权衡,需结合实际场景合理应用。
TD 权衡与挑战
张量分解虽能大幅提升效率,但需权衡分解秩、计算复杂度和数值稳定性。
- 秩选择:秩过小信息损失大,过大压缩有限。不同分解方法对秩的定义不同,需结合实际调优。
- 分解计算开销:分解本身需迭代优化,推理时需重构张量,可能增加延迟。
- 数值稳定性:高相关结构或分解方法不当易导致数值不稳定,可通过正则化等手段缓解。
尽管如此,张量分解在内存和计算受限场景下仍是极具价值的优化工具。自适应分解、自动秩选择、硬件感知分解等新方法不断提升其实用性。下节将总结低秩分解与张量分解的核心洞见。
LRMF 与 TD 对比
低秩分解和张量分解均通过低秩近似降低模型复杂度,但应用场景、计算权衡和结构假设各异。下表对比两者主要特性:
| 特性 | 低秩矩阵分解(LRMF) | 张量分解 |
|---|---|---|
| 适用数据结构 | 二维矩阵 | 多维张量 |
| 压缩机制 | 分解为两个或多个低秩矩阵 | 分解为多个低秩张量组件 |
| 常用方法 | SVD、ALS | CP、Tucker、TT |
| 计算复杂度 | 较低,秩为 $k$ 时约 $O(mnk)$ | 更高,需迭代优化和张量收缩 |
| 存储压缩 | $O(mn) \to O(mk + kn)$ | 压缩更强,但存储结构更复杂 |
| 推理开销 | 需额外一次矩阵乘法 | 需额外张量操作,可能增加推理延迟 |
| 主要应用 | 全连接层、嵌入、推荐系统 | 卷积核、注意力机制、多模态学习 |
| 实现复杂度 | 易于实现,常用直接分解 | 更复杂,需迭代优化和秩选择 |
两者可结合应用于同一模型,不同结构采用不同分解方式,实现整体最优压缩。
神经架构搜索(NAS)
剪枝、蒸馏等方法依赖人工经验确定最优结构,需大量试错。神经架构搜索(NAS)通过自动化探索大规模结构空间,系统性地发现兼顾精度、计算、内存和延迟的最优架构。
图 12 展示了 NAS 流程。NAS24 包括三阶段:定义搜索空间(结构组件与约束)、应用搜索策略(强化学习、进化算法、梯度法等)探索候选架构,并评估其性能,确保满足精度与效率目标。NAS 能自动发现超越人工设计的新型高效结构,大幅减少专家工作量。

NAS 搜索策略多样,包括强化学习(RL)、进化算法、梯度法等。RL 将结构选择建模为序列决策,精度为奖励信号;进化算法通过变异和交叉进化架构族群;梯度法则将结构参数连续化,极大降低搜索成本。
模型效率编码
NAS 包含三大阶段:定义搜索空间、探索候选架构、评估性能。搜索空间决定可修改的结构组件与约束,搜索策略指导探索,评估过程确保架构满足多目标需求(精度、效率、硬件适配)。
- 搜索空间定义:确定可修改的层类型、卷积方式、激活函数、硬件优化等,平衡创新性与可计算性。
- 搜索策略:采用 RL、进化、梯度等方法,结合历史表现选择最优架构。
- 评估标准:综合精度、FLOPs、内存、延迟、能耗等多维指标,确保架构适配部署需求。
NAS 实现了结构设计与优化一体化,自动发现兼具高精度与高效率的架构。
搜索空间定义
NAS 首先需确定可探索的结构空间。空间过小限制创新,过大则计算不可承受。典型搜索空间以模块化组件为基础,包括层类型(标准卷积、深度可分离卷积、注意力、残差块等)、网络深度与宽度、激活函数(ReLU、Swish、GELU 等)、核大小、感受野、跳连等。部分 NAS 还集成硬件感知优化,确保架构适配目标硬件(GPU、TPU、移动 CPU)。
合理的搜索空间既能激发创新,又能控制计算成本。
搜索空间探索
确定空间后,NAS 需高效探索不同架构。搜索策略需平衡探索(尝试新结构)与利用(优化已有结构)。
主流方法包括:
- 强化学习:将结构选择建模为决策过程,精度为奖励,逐步生成更优架构。计算成本高。
- 进化算法:维护架构族群,通过变异、选择、交叉进化,适合并行计算。
- 梯度法:将结构参数连续化,权重与结构参数联合优化,极大降低搜索成本。
搜索策略直接影响 NAS 的可行性。早期 RL-NAS 需数周 GPU 计算,梯度法如 DARTS 将成本降至 1-4 天。
候选架构评估
每个候选架构需基于多维指标评估。除精度外,NAS 还需优化效率约束,确保模型可部署。主要评估指标包括计算复杂度(FLOPs)、内存、推理延迟、能耗25。如 FBNet26 通过延迟约束优化移动端推理。
集成这些约束,NAS 能系统性发现兼顾精度、效率、硬件适配的架构。
NAS 优化问题
NAS 可建模为双层优化问题:外层搜索结构,内层训练权重。形式化为:
$$ \alpha^* = \arg\min_{\alpha \in \mathcal{A}} \mathcal{L}{\text{val}}(w^*(\alpha), \alpha) \quad \text{约束} \quad C(\alpha) \leq C{\text{max}} $$
其中 $w^*(\alpha)$ 为结构 $\alpha$ 的最优权重,需最小化训练损失。
搜索空间即便仅 10 个选项/层、20 层,也有 $10^{20}$ 种结构,穷举不可行。高效 NAS 需合理空间、搜索策略和加速评估。
搜索空间设计
空间设计需结合领域知识,聚焦高潜力区域,兼顾灵活性。
基于 Cell 的空间:仅搜索可复用的计算单元(cell),如卷积 cell,极大降低空间规模。EfficientNet 即采用此法。
硬件感知空间:将延迟等部署约束纳入目标,直接优化实际硬件延迟(如 MobileNetV3 用延迟预测模型)。
搜索策略
不同策略在效率、多样性和最优性间权衡,见下表:
| 策略 | 搜索效率 | 适用场景 | 主要挑战 |
|---|---|---|---|
| 强化学习 | 400-1000 GPU 天 | 新领域、无约束搜索 | 计算成本高 |
| 进化算法 | 200-500 GPU 天 | 有并行基础设施 | 需大族群 |
| 梯度法(DARTS) | 1-4 GPU 天 | 计算预算有限 | 可能收敛于次优 |
NAS 实践
硬件感知 NAS 直接优化实际部署指标。MnasNet 搜索目标为:
$$ \text{Reward}(\alpha) = \text{Accuracy}(\alpha) \times \left(\frac{L(\alpha)}{L_{\text{target}}}\right)^\beta $$
$L(\alpha)$ 为实际延迟,$L_{\text{target}}$ 为目标延迟,$\beta$ 控制权衡。MnasNet 发现变扩展比的倒残差结构优于人工设计。
何时使用 NAS
NAS 适用于新硬件平台、超大规模部署(亿级推理)、多配置架构族等场景。标准部署或预算有限时,优先采用现有 NAS 架构(如 EfficientNet、MobileNetV3、MnasNet)。
架构示例
NAS 已成功设计出多款高效架构,如 EfficientNet(复合缩放)、MobileNetV3(倒残差+SE)、FBNet(移动端延迟优化)、NAS-BERT(高效 Transformer)、ViT 等。它们均通过自动化权衡结构优化、计算与内存效率、硬件适配,取得超越人工设计的表现。
模型结构优化可带来巨大提升。例如,通过结构化剪枝和蒸馏,BERT-Base 从 440MB 压缩至 110MB,参数减少 75%,精度仅下降 0.8%。但移动端推理仍达不到 50ms 目标,实际为 120ms。
分析发现,虽然参数减少 75%,但每次矩阵乘法仍用 FP32,每参数 4 字节,移动端内存带宽远低于服务器 GPU,成为瓶颈。结构已优化,数值表示未变,需进一步降低精度。
这说明,结构优化仅是效率提升的第一步。数值精度优化(如 FP32→INT8)可将内存流量降 4 倍,利用专用整数单元,推理速度提升 4-8 倍。结构与数值优化协同,才能实现端到端效率提升。
如剪枝后 BERT 110MB,进一步量化为 INT8 后仅 28MB,推理延迟降至 45ms,最终达标。量化补齐了结构优化的最后一环。
量化与精度优化
模型结构优化决定“做什么计算”,而计算效率高度依赖数值精度——优化框架的第二维。
数值精度决定权重与激活的表示方式,直接影响内存使用、计算效率和功耗。许多最先进的模型使用高精度浮点格式如 FP32(32 位浮点),虽然提供了数值稳定性和高精度,但也增加了存储需求、内存带宽使用和功耗。现代 AI 加速器包括专用硬件支持低精度计算,使得 FP16 和 INT8 操作的吞吐量远高于 FP32。降低精度会引入量化误差,可能降低精度,具体影响取决于模型架构、数据集特性和硬件支持。
精度优化技术主要分为三类:
- 后训练量化:在模型训练完成后,快速将模型权重和激活值转换为低精度表示,便于快速部署。
- 量化感知训练:在训练过程中模拟低精度推理,调整模型权重以适应量化带来的误差,适用于对精度要求较高的生产环境。
- 极端量化:如二值化(Binarization)和三值化(Ternarization),将权重和激活值压缩为极少数离散值,适合资源极其受限的环境。
本节将探讨不同精度格式的权衡、硬件与软件协同设计的考量,以及在最大化效率增益的同时,最小化精度下降的方法。
精度与能耗
高效数值表示可大幅降低存储、计算延迟和能耗,尤其适合移动 AI、嵌入式系统和云推理。精度水平可针对特定硬件能力调优,最大化 GPU、TPU、NPU 和边缘 AI 芯片的吞吐量。
能耗成本
不同数值精度的能耗差异显著。如下图(图 13)所示,32 位浮点加法约需 0.9 pJ,16 位仅 0.4 pJ,32 位整数加法 0.1 pJ,8 位仅 0.03 pJ。大规模模型累计可节省大量能耗,助力 第 18 章:可持续 AI 。量化带来的能效提升,也有助于 第 15 章:安全与隐私 的安全防护。

更重要的是,降低精度还能极大减少内存能耗。低精度表示降低了存储和带宽需求,减少了高能耗的内存访问,尤其是 DRAM(1.3–2.6 nJ)远高于缓存(如 L1 8KB 仅 10 pJ)。数据流动的能耗常远超计算本身,优化精度可显著降低整体系统功耗,尤其适合硬件加速和边缘设备。
性能提升
下图(图 14)通过堆叠柱状图和双轴展示了量化对推理时间和模型体积的影响。每组左侧柱体表示从 FP32 到 INT8 后推理时间的提升,右侧柱体则展示模型体积的缩减。结果显示,量化模型推理速度最高可提升 $4\times$,存储需求也降低 $4\times$,非常适合资源受限环境部署。

但降低数值精度也带来权衡。低精度格式可能引入数值不稳定和量化噪声,影响模型精度。有些架构(如大型 Transformer NLP 模型)对量化较为稳健,而部分模型则可能精度下降明显。因此,选择合适的数值精度需在精度约束、硬件支持和效率提升之间权衡。
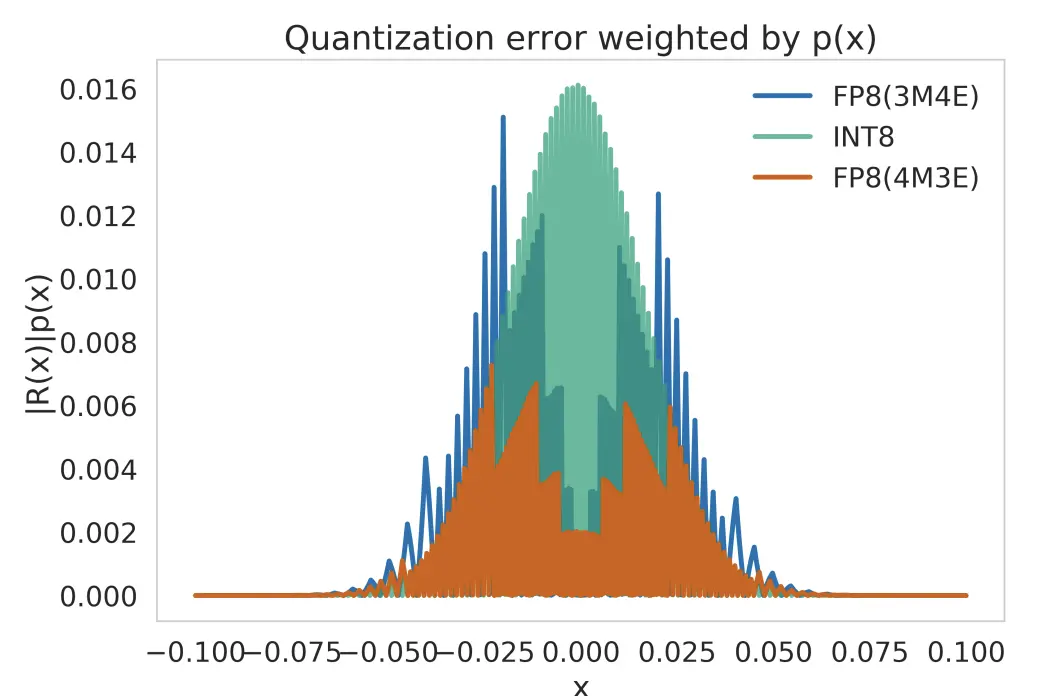
图 15 展示了不同数值格式(FP8 各变体与 INT8)下,量化误差随概率分布加权的情况。误差分布揭示了不同格式在数值区间内引入的量化噪声差异,这直接影响模型的精度与稳定性。
数值编码与存储
机器学习系统中的数值数据表示不仅仅是精度问题,还涉及编码格式和存储机制,这些都对计算效率有重要影响。数值编码决定了浮点和整数在内存中的存储方式及硬件处理方式,直接影响 ML 工作负载的性能。随着模型规模和复杂度提升,优化数值编码对于高效利用专用硬件变得愈发重要。
浮点数表示广泛采用 IEEE 754 标准 ,通过符号位、指数位和尾数位组合编码。常见的 FP32(单精度)、FP64(双精度)精度高但资源消耗大。为提升效率,业界引入了低精度格式如 FP16、 bfloat16 、 FP8 等,既降低存储需求,又能满足 ML 计算的动态范围。bfloat16 与 FP16 不同,保留了与 FP32 相同的 8 位指数,牺牲部分尾数精度,因而在训练中能更好地保持数值稳定性,适合大规模梯度更新。
整数表示(如 INT8、INT4)进一步简化存储和计算,省去了指数和尾数编码,常用于推理阶段的量化模型。权重和激活被离散化为整数,便于硬件加速和降低功耗,尤其适合边缘和移动设备。极端情况下,二值化和三值化仅用 1-2 位表示,极大压缩模型体积和能耗,但需配合专用训练或结构调整以减缓精度损失。
新兴数值格式力图在效率与精度间取得更好平衡。例如 TF32 (NVIDIA Ampere GPU 专用)缩减了 FP32 的尾数位,保留指数宽度,实现更快计算且精度损失极小。FP8 作为 AI 加速器的新宠,进一步降低精度但结构上更适合 ML 负载。其他如 Posit 、 Flexpoint 、 BF16ALT 等格式也在探索数值稳定性和硬件适配性。
数值编码效率还受数据在内存中的存储与访问方式影响。AI 加速器通过优化内存层级、专用硬件(如张量核、矩阵乘法单元、向量处理引擎)提升低精度计算性能。数据对齐、内存分块、压缩等技术确保低精度计算带来实际性能提升。
随着 ML 系统演进,数值编码与存储策略将持续适应大模型和多样化硬件需求。新一代 AI 精度格式的不断发展,凸显了数值表示与硬件协同设计的重要性,确保模型在降低计算成本的同时实现最优性能。
数值格式对比
下表(表 7)对比了机器学习常用的数值精度格式,涵盖存储效率、计算速度和能耗等权衡。FP8、TF32 等新格式专为 AI 加速器优化。
| 精度格式 | 位宽 | 存储压缩(相对 FP32) | 计算速度(相对 FP32) | 功耗 | 典型应用场景 |
|---|---|---|---|---|---|
| FP32(单精度浮点) | 32 位 | 基线(1×) | 基线(1×) | 高 | 通用训练与推理 |
| FP16(半精度浮点) | 16 位 | 2× 更小 | FP16 优化硬件上快 2× | 低 | 加速训练、推理(NVIDIA Tensor Cores、TPU) |
| bfloat16(脑型浮点) | 16 位 | 2× 更小 | 与 FP16 类似,动态范围更大 | 低 | TPU 训练、Transformer 等模型 |
| TF32(TensorFloat-32) | 19 位 | 近似 FP16 大小 | NVIDIA Ampere GPU 上快至 8× | 低 | NVIDIA GPU 训练 |
| FP8(8 位浮点) | 8 位 | 4× 更小 | 某些场景下比 INT8 更快 | 显著更低 | 高效训练/推理(H100、AI 加速器) |
| INT8(8 位整数) | 8 位 | 4× 更小 | 比 FP32 快 4–8× | 显著更低 | 量化推理(边缘 AI、移动 AI、NPU) |
| INT4(4 位整数) | 4 位 | 8× 更小 | 依赖硬件 | 极低 | 超低功耗 AI、实验性量化 |
| 二值/三值(1/2 位) | 1–2 位 | 16–32× 更小 | 高度依赖硬件 | 最低 | 极致高效(Binary/Ternary 神经网络) |
FP16、bfloat16 在保持精度的同时提升效率。许多 AI 加速器(如 NVIDIA Tensor Cores、TPU)专门支持 FP16,矩阵运算速度提升 2 倍。bfloat16 保留 FP32 的 8 位指数,尾数仅 7 位,动态范围(约 $10^{-38}$ 到 $10^{38}$)与 FP32 相当但精度略低。FP16 指数仅 5 位,动态范围(约 $10^{-5}$ 到 $10^5$)大幅收窄,更适合推理。bfloat16 能更好应对训练中的极值,FP16 则易下溢/上溢,适合推理或需精心缩放的训练。下图(图 16)直观展示了位宽分配对精度与数值范围的影响。\footnote{浮点格式的动态范围由指数位宽和偏置决定。FP32、bfloat16 均为 8 位指数,偏置 127,指数范围 $[-126,127]$,数值范围约 $10^{-38}$ 到 $10^{38}$。FP16 指数 5 位,偏置 15,指数范围 $[-14,15]$,数值范围约 $10^{-5}$ 到 $10^5$。FP16 动态范围更窄,训练易数值不稳定,bfloat16 保持 FP32 的宽广范围,更适合深度网络训练。}

INT8 精度在推理场景下提升更为显著。许多量化模型采用 INT8 推理,存储降 4 倍,计算加速 4–8 倍,广泛应用于移动和嵌入式 AI。
二值/三值网络是量化的极致,权重和激活仅取 1 位或 2 位,极大节省存储和能耗,但若无专用结构,精度损失较大。
精度降低的权衡
降低数值精度可带来显著效率提升,包括内存占用、功耗和吞吐量,但也会引入数值误差和量化噪声,影响模型精度。影响程度取决于模型结构、数据集和具体精度格式。
不同模型对量化的容忍度不同。大规模 CNN、Transformer 等架构即便采用 bfloat16 或 INT8 也能保持高精度;而小模型或对数值精度要求高的任务则更易受影响。网络不同层对精度降低的敏感度也不同,如 BN、注意力机制等更易受影响。因此,混合精度训练(不同层用不同精度)可在保证精度的同时提升效率。
硬件支持也是关键。GPU、TPU、NPU 等 AI 加速器内置低精度运算单元,能高效执行 FP16、bfloat16、INT8 甚至 FP8 运算,提升速度和能效。通用 CPU 通常缺乏专用低精度指令,量化收益有限。新格式如 TF32、FP8 则为非极端量化硬件提供了更优折中。
此外,低精度运算可降低功耗,减少内存访问和简化计算,尤其适合移动和边缘 AI。极端低精度(如 INT4、二值/三值)可进一步降低功耗和存储,但需专用结构以弥补精度损失。
为减缓精度下降,可采用多种量化策略。最终,选择何种精度需在效率与精度之间权衡,结合模型结构、应用需求和硬件支持。通过软硬件协同优化,可在保持性能的同时最大化效率。
精度降低策略
降低数值精度是提升模型效率的重要手段。通过减少权重和激活的位宽,模型可降低内存占用、提升吞吐量、降低功耗。但简单量化易引入误差,导致精度下降。为此,业界发展出多种精度优化策略,实现效率与精度的平衡。
量化可在模型生命周期的不同阶段应用。后训练量化(PTQ)在训练后降低精度,适合快速推理优化。量化感知训练(QAT)在训练中模拟量化,提升低精度下的精度。混合精度训练则结合硬件支持,动态分配不同运算精度,实现高效推理。
下图(图 17)将量化技术按实现复杂度、资源需求和应用场景分为三层,便于理解和选择。

后训练量化(PTQ)
量化是突破内存瓶颈、降低带宽的核心算法。主流 ML 框架(TensorFlow Lite、ONNX Runtime、PyTorch)均内置标准化 PTQ API,便于高效落地。
PTQ 在训练后将权重和激活从高精度(FP32)转换为低精度(INT8/FP16),无需重新训练。这样可显著减小模型体积、加速推理、降低能耗,适合移动、边缘和云推理等资源受限场景。
PTQ 最大优势是计算成本低——无需重训练或访问训练数据。但降低精度会引入量化误差,尤其对高精度需求任务影响较大。
PTQ 工作原理
PTQ 将训练好的模型权重和激活从高精度浮点(如 FP32)转换为低精度(如 INT8/FP16),减少模型内存占用、加速推理、降低功耗。但低精度格式数值范围更小,量化会引入舍入误差,影响精度。
核心机制是缩放并映射高精度值到低精度区间。常用的均匀量化(uniform quantization)用统一缩放因子将浮点值映射为整数。公式如下: $$ q = \text{round} \left(\frac{x}{s} \right) $$ 其中:
- $q$ 为量化后的整数,
- $x$ 为原始浮点值,
- $s$ 为缩放因子,将浮点区间映射到整数区间。
代码示例(FP32→INT8 均匀量化):
import torch
# 原始 FP32 权重
weights_fp32 = torch.tensor(
[0.127, -0.084, 0.392, -0.203], dtype=torch.float32
)
print(f"Original FP32: {weights_fp32}")
print(f"Memory per weight: 32 bits")
# 步骤 1:计算缩放因子
max_val = weights_fp32.abs().max()
scale = max_val / 127 # INT8 最大正值为 127
# 步骤 2:量化 q = round(x/s)
weights_int8 = torch.round(weights_fp32 / scale).to(torch.int8)
print(f"Quantized INT8: {weights_int8}")
print(f"Memory per weight: 8 bits (reduced from 32)")
# 步骤 3:反量化验证
weights_dequantized = weights_int8.float() * scale
print(f"Dequantized: {weights_dequantized}")
print(
f"Quantization error: "
f"{(weights_fp32 - weights_dequantized).abs().mean():.6f}"
)
该示例展示了每个权重从 32 位压缩到 8 位,且量化误差极小。
如 INT8 量化中,模型浮点值(如 $[-r, r]$)被映射到整数区间 $[-128, 127]$。缩放因子确保信息尽量保留。量化后推理用整数运算,效率远高于浮点,但因舍入和近似,精度略有下降。
除均匀量化外,非均匀量化可为高密度区间分配更高精度,适合权重分布集中场景,但实现更复杂,常用于对精度极为敏感的模型。
PTQ 对 CV 模型(如 CNN)效果尤佳,NLP Transformer、语音识别等对数值微小变化敏感的模型则需更精细的量化策略。
校准(Calibration)
PTQ 的关键步骤是校准,即选择最优的裁剪区间 [$\alpha$, $\beta$]。校准通过代表性数据集估算权重和激活的分布,确定量化区间,最大限度减少信息损失。
下图(图 18)展示了 PTQ 流程:以预训练模型为起点,使用校准数据集估算分布,确定裁剪区间,量化生成高效模型。

常见校准方法
- 最大值法(Max):取校准期间的最大绝对值为裁剪区间,简单但易受异常值影响。如图 19 所示,激活分布有长尾,最大值法可能导致区间过大。
- 熵法(Entropy):最小化原始浮点分布与量化分布的信息损失(如 KL 散度),TensorRT 默认采用,适合保持分布特征。
- 分位数法(Percentile):按绝对值分布设定区间,如 99% 校准裁剪掉最大 1% 的值,避免异常值影响。
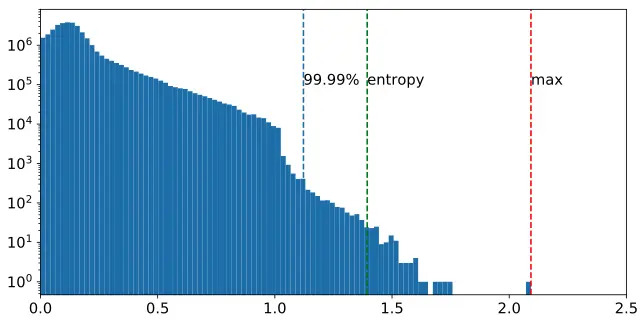
校准质量直接影响量化模型性能。校准区间分为:
- 对称校准:区间以零为中心,正负区间等比例缩放,适合分布居中数据。
- 非对称校准:区间不对称,正负区间缩放不同,适合分布偏移数据。
合理选择校准方法和区间,是兼顾精度与效率的关键。
校准区间
PTQ 的难点在于如何选择合适的裁剪区间 $[\alpha, \beta]$。如 图 20 所示,主要有对称和非对称两种策略。

左图为对称校准,区间 $[-1, 1]$ 映射到 $[-127,127]$,实现实现简单但对偏移分布不友好。右图为非对称校准,区间 $[-0.5, 1.5]$,零点偏移,适合分布偏移场景,但实现更复杂。
- 对称校准适合权重分布居中模型,计算和硬件实现简单。
- 非对称校准适合分布偏移模型,能更好利用量化区间,但需额外计算。
主流框架(如 TensorRT、PyTorch)均支持两种模式,建议结合实际分布选择。
量化粒度
确定裁剪区间后,还需优化量化粒度以提升精度。以 CNN 为例,不同卷积核的输入激活区间差异大,需分别量化以减少精度损失。
如 图 21 所示,不同卷积核(Filter 1 与 Filter 3)区间差异明显,需细粒度量化。

常见粒度包括:
- 层级量化(Layerwise):全层共用区间,简单但精度损失大。
- 分组量化(Groupwise):按组共享区间,适合分布差异大的层,精度提升但计算开销增加。
- 通道量化(Channelwise):每个卷积核独立区间,精度最佳,主流实践采用。
- 子通道量化(Sub-channelwise):每个卷积核再细分,精度极高但计算开销大,仅用于极端场景。
通道量化在精度与效率间取得最佳平衡,已成为主流。
权重量化与激活量化
权重量化将高精度权重(如 Float32)转换为低精度(如 INT8),如 图 22 所示,极大降低模型体积和推理资源消耗。

激活量化则在推理时对中间输出进行量化,进一步加速低精度硬件推理。近年来,激活感知权重量化(AWQ)等新方法通过关注激活分布,仅保护极少数关键权重,提升大模型压缩与加速效果(参考 Ji Lin 等,2023)。
静态与动态量化
确定量化区间类型和粒度后,还需决定量化区间的计算时机。主要有静态量化和动态量化两种。
- 静态量化:量化区间在推理前预先计算,推理时无需额外计算,效率高但精度略低。常用校准输入估算区间。
- 动态量化:推理时实时计算区间,能针对每个输入自适应,精度更高但计算开销大,适合对精度极为敏感的场景。
下表(表 8)总结了 PTQ、QAT 和动态量化的特点及权衡,便于选择合适的量化策略。
| 方面 | 后训练量化(PTQ) | 量化感知训练(QAT) | 动态量化 |
|---|---|---|---|
| 优点 | |||
| 简单易用 | ✓ | ✗ | ✗ |
| 精度保持 | ✗ | ✓ | ✓ |
| 自适应性 | ✗ | ✗ | ✓ |
| 性能优化 | ✗ | ✓ | 视情况而定 |
| 缺点 | |||
| 精度下降 | ✓ | ✗ | 视情况而定 |
| 计算开销 | ✗ | ✓ | ✓ |
| 实现复杂度 | ✗ | ✓ | ✓ |
| 权衡 | |||
| 速度 vs 精度 | ✓ | ✗ | ✗ |
| 精度 vs 成本 | ✗ | ✓ | ✗ |
| 自适应 vs 开销 | ✗ | ✗ | ✓ |
PTQ 的主要优点在于其低计算成本,因为它不需要重新训练模型。这使得 PTQ 成为训练完成后快速部署模型的一个有吸引力的选择,特别是在重新训练计算开销大或不可行的情况下。由于 PTQ 仅修改权重和激活的数值表示,因此可以广泛应用于各种预训练模型,而无需对模型架构进行修改。
PTQ 还通过降低模型参数的位宽,显著节省内存和存储。例如,将模型从 FP32 转换为 INT8 可以实现$4\times$的存储大小减小,使其能够在资源受限的设备上部署更大规模的模型,如移动电话、边缘 AI 硬件和嵌入式系统。这种内存占用的减少也降低了通过网络传输模型时的带宽需求。
在计算效率方面,PTQ 允许使用整数算术进行推理,而整数运算在许多硬件平台上本质上比浮点运算快。TPU 和神经处理单元(NPU)等 AI 加速器针对低精度计算进行了优化,从而在执行量化模型时实现更高的吞吐量和更低的功耗。这使得 PTQ 特别适用于需要实时推理的应用场景,如自动驾驶系统中的物体检测或移动设备上的语音识别。
PTQ 挑战与局限
尽管 PTQ 具有诸多优点,但由于浮点值到离散低精度表示的映射过程中的舍入效应,它引入了量化误差。虽然有些模型对这些变化具有稳健性,但其他模型可能会经历显著的精度下降,特别是在依赖于数值精度较高的任务中。
这种精度损失的程度取决于模型架构和任务领域。用于图像分类的 CNN 对 PTQ 通常具有较好的容忍度,即使在激进的 INT8 量化下也能保持接近原始的精度。而在 NLP 和语音识别中使用的基于 Transformer 的模型则往往更为敏感,因为这些架构依赖于注意力机制中数值关系的精确性。
为了减轻精度损失,通常采用 KL 散度缩放或按通道量化等校准技术来微调缩放因子,尽量减少信息损失。一些框架(包括 TensorFlow Lite 和 PyTorch)提供了带有内置校准方法的自动量化工具,以提高精度保留。
另一个 PTQ 的局限是并非所有硬件都支持高效的整数运算。虽然 GPU、TPU 和专用的边缘 AI 芯片通常包括对 INT8 推理的专门支持,但通用 CPU 可能缺乏低精度执行的优化指令,从而导致量化性能提升有限。
PTQ 通常不适用于训练过程。由于 PTQ 是在训练后应用量化的,因此需要进一步微调或适应的模型可能更适合采用其他方法,如量化感知训练(QAT),以确保在学习过程中充分考虑精度约束。
后训练量化仍然是提高推理效率的最实用和广泛使用的技术之一。它通过显著降低计算和存储需求,提供了在资源受限环境中部署机器学习模型的可行方案。然而,PTQ 的成功依赖于模型架构、任务敏感性和硬件兼容性。在精度下降不可接受的场合,可能需要采用量化感知训练等替代策略。
后训练量化为更高级的量化方法奠定了基础。量化感知训练(QAT)通过在训练过程中直接整合量化约束,模拟低精度算术运算,使模型适应量化效应,尤其适用于对数值精度要求较高的模型,如用于 NLP 和语音识别的变换器。图 23 说明了 QAT 过程:对预训练模型应用量化,然后进行微调以适应低精度约束。

在许多情况下,QAT 还可以基于 PTQ 进行,如图 24 所示。首先应用 PTQ 生成初始量化模型,然后以该量化模型为基础进行 QAT 微调,帮助模型更好地适应低精度约束。这种结合 PTQ 和 QAT 的混合方法,兼顾了效率和精度,减少了单独采用后训练量化时通常会出现的精度下降。

训练数学
在前向传播过程中,权重和激活被量化和反量化,以模拟降低精度的效果。通常表示为: $$ q = \text{round} \left(\frac{x}{s} \right) \times s $$ 其中 $q$ 表示模拟的量化值,$x$ 表示全精度的权重或激活,$s$ 是将浮点值映射到低精度整数的缩放因子。
尽管前向传播使用了量化值,但反向传播中的梯度计算仍然是全精度的。这是通过直通估计器(STE)实现的,该估计器通过将量化操作的导数视为一来近似量化函数的梯度。这样可以防止由于量化操作的不可微性而阻碍梯度传播,从而实现有效的模型训练。
直通估计器(STE):用于非光滑函数(如量化函数)的梯度近似技术。将量化操作的梯度视为 1,使得反向传播能够通过量化层。尽管在理论上存在局限性,但在实践中对训练二值神经网络和量化感知训练至关重要。
在训练过程中整合量化效应,使模型学习到最佳的权重和激活分布,从而最小化数值精度损失的影响。这样训练出的模型在部署时使用真实的低精度算术(如 INT8 推理)时,能显著高于后期量化的模型。
QAT 优势
QAT 的主要优点是其在低精度推理条件下保持模型精度的能力。通过在训练中整合量化,模型能够补偿精度损失,减少舍入误差和数值不稳定的影响。这对于在 NLP、语音识别和高分辨率计算机视觉中常用的对量化敏感的模型尤为重要。
另一个主要好处是,QAT 允许在硬件加速器上进行低精度推理,而不会显著降低精度。TPU、NPU 和专用边缘设备等 AI 处理器包括整数运算的专用硬件,使得 INT8 模型相比 FP32 模型具有更快的推理速度和更低的能耗。考虑到量化效应的训练确保了最终模型能够充分利用这些硬件优化。
QAT 挑战与权衡
尽管 QAT 具有诸多优点,但在训练过程中会增加额外的计算开销。每次前向传播都进行量化模拟,相比全精度方法,训练速度会变慢。这一过程也增加了训练调度的复杂性,使得 QAT 在大规模模型上的应用变得不够实际,因为额外的训练时间可能是不可接受的。
QAT 还引入了额外的超参数和设计考虑,例如选择合适的量化方案和缩放因子。与训练后量化(PTQ)不同,QAT 需要仔细调整训练动态,以确保模型适应低精度约束。
下表(表 9)总结了 QAT 与 PTQ 的主要权衡:
| 方面 | 量化感知训练(QAT) | 后训练量化(PTQ) |
|---|---|---|
| 精度保留 | 最小化量化带来的精度损失 | 可能会出现精度下降 |
| 推理效率 | 针对低精度硬件(如 TPU 上的 INT8)优化 | 优化但可能需要校准 |
| 训练复杂度 | 需要在量化约束下重新训练 | 无需重新训练 |
| 训练时间 | 由于前向传播中模拟量化而变慢 | 较快,因为量化是事后处理的 |
| 部署准备 | 最适合对量化误差敏感的模型 | 快速优化模型以进行推理 |
将量化整合到训练过程中的主要好处是,它比后训练量化更有效地保持模型精度,尤其是在低精度推理条件下。通过在训练中考虑量化效应,模型能够适应低精度算术运算,从而减少量化误差。尽管 QAT 在低精度下实现更高的精度,但它需要额外的训练时间和计算资源。在实践中,通常采用从 PTQ 开始的混合方法,对于对精度要求较高的模型再应用 QAT,以在效率和性能之间取得最佳平衡。
极端量化
超越 INT8 和 INT4 的极端量化技术使用 1 位(二值化)或 2 位(三值化)表示法,实现内存使用和计算需求的剧减。二值化将权重和激活限制为两个值(通常是 -1 和 +1,或 0 和 1),大幅减少模型大小,并在专用硬件(如二值神经网络)上加速推理。然而,这种限制严重限制了模型的表达能力,往往会降低在图像识别或自然语言处理等任务上的精度。
三值化通过允许三个值(-1、0、+1)扩展了二值化,提供了额外的灵活性,略微提高了精度。零值的引入使得稀疏性更强,同时保持了更多的表达能力。这两种技术都需要像直通估计器(STE)这样的梯度近似方法来处理训练过程中不可微的量化操作,QAT 的结合有助于减轻精度损失。
挑战与局限
尽管能够为嵌入式系统和移动设备实现超低功耗的机器学习,二值化和三值化仍面临着重大挑战。保持性能在如此极端的量化下变得困难,需要专用硬件高效处理二进制或三元操作。传统处理器缺乏对这些计算的优化,迫使开发定制硬件加速器。
精度损失仍然是一个关键问题。这些方法适用于对精度要求不高的任务,或者可以通过 QAT 弥补精度限制的场景。尽管面临挑战,但在保持可接受精度的同时大幅减少模型大小的能力,使它们在边缘 AI 和资源受限环境中具有吸引力。未来专用硬件和训练技术的进步,可能会增强它们在高效、可扩展 AI 中的作用。
多技术优化策略
在探讨了量化技术(PTQ、QAT、二值化和三值化)、剪枝方法和知识蒸馏后,我们现在研究如何系统地结合这些互补方法,以实现更优的优化结果。通过综合不同的优化维度,集成策略利用了各种技术之间的协同作用,最大限度地提高效率提升,同时保持模型精度。
每种优化技术针对模型效率的不同方面:量化降低数值精度,剪枝消除冗余参数,知识蒸馏将能力转移到紧凑架构,神经架构搜索(NAS)优化结构设计。这些技术具有互补特性,使其能够实现强大的组合效果。
剪枝和量化的协同效应在于,剪枝减少了参数数量,而量化降低了精度,从而产生了乘法压缩效果。先进行剪枝可以减少参数集,从而使后续的量化更有效,并减少寻找最佳量化策略的搜索空间。这种顺序方法可以实现超过单独使用任何一种技术的压缩比。
知识蒸馏与量化的有效集成,通过减轻激进量化带来的精度损失,增强了模型的稳健性。该方法通过训练学生模型匹配教师模型的行为,而不仅仅是最小化任务损失,特别适用于极端量化场景,在这些场景中,直接量化可能导致不可接受的精度下降。
神经架构搜索使得协同设计成为可能,专门针对量化约束优化模型结构,识别在低精度操作下保持精度的架构。这种共设计方法生成的模型,天生就适合后续的量化和剪枝优化,提高了这两种技术的有效性。
如图 25 所示,剪枝、量化和奇异值分解(SVD)等不同压缩策略在模型大小和精度损失之间表现出不同的权衡。剪枝与量化结合(红色圆圈)相比于单独量化(黄色方块)也提供了合理的平衡。相比之下,SVD(绿色菱形)则需要更大的模型尺寸才能维持精度,说明不同技术对压缩效果的影响。

量化不同于剪枝、知识蒸馏和 NAS,因为它专注于降低权重和激活的数值精度。尽管单独的量化可以提供显著的计算效益,但当与剪枝、蒸馏和 NAS 等互补技术结合时,其有效性可以得到增强。这些方法针对模型效率的不同方面协同工作,创造出更紧凑、更快、能效更高的模型,从而在受限环境中实现更好的性能。
我们的优化之旅仍在继续。我们通过结构化剪枝和知识蒸馏将 BERT-Base 从 440MB 剪至 110MB,然后量化为 INT8,将模型缩减至 28MB,推理延迟从移动硬件上的 120ms 降至 45ms。这些优化使一个不可用的模型接近于可部署状态。然而,分析发现了一个令人困惑的低效:理论 FLOP 计数表明推理应在 25ms 内完成,但实际执行却需要 45ms。剩余的 20ms 消失到哪里去了?
详细分析揭示了答案。尽管量化降低了精度,但模型仍然计算了不必要的零值。结构化剪枝移除了整个注意力头,但剩余的稀疏权重矩阵仍以密集格式存储,浪费了内存带宽和计算资源。层归一化操作按顺序运行,尽管它们本质上是可以并行的。模型对所有输入的处理方式相同,即使简单输入也可以在浅层提前退出。GPU 有 40% 的执行时间处于空闲状态,等待内存传输而不是执行操作。
这些观察结果揭示了模型表示和数值精度优化虽然必要,但仍然不够。表示技术决定了执行哪些计算,精度技术决定了单个操作如何执行。但没有解决计算如何组织和调度以最大化硬件利用率。这是架构效率优化的领域,也是我们框架的第三个维度。
架构效率技术转变了执行模式。通过专用内核利用稀疏性消除对修剪权重的计算。操作融合将顺序操作(层归一化、注意力、前馈)合并为单个 GPU 内核,减少 40% 的内存流量。动态计算使简单输入在经过 6 层后就可以退出,而不必处理所有 12 层。硬件感知调度并行化操作,以保持 GPU 高利用率。将这些技术应用于我们优化后的 BERT 模型,将推理时间从 45ms 降至 22ms,最终实现 25ms 的理论目标,使部署真正可行。
这一进展说明了为什么所有三个优化维度必须协同工作。模型表示提供结构效率(更少的参数),数值精度提供计算效率(低精度算术),架构效率提供执行效率(优化调度和硬件利用)。只有在系统地解决所有维度时,复合效应(440MB/120ms → 28MB/22ms,内存减少 16 倍,延迟改善 5.5 倍)才能实现。
架构效率技术
架构效率优化确保计算在目标硬件上高效执行,通过将模型操作与处理器能力和内存层次结构对齐。与表示优化(决定执行哪些计算)和精度优化(决定数值保真度)不同,架构效率关注操作的调度方式、内存访问方式以及工作负载如何适应输入特征和硬件约束。
这一优化维度对于资源受限场景尤为重要(参见 第 14 章:设备端学习 ),因为剪枝和量化带来的理论 FLOP 减少可能在没有架构修改的情况下无法转化为实际的速度提升。以密集格式存储的稀疏权重矩阵浪费了内存带宽。尽管它们本质上是可以并行的,顺序执行的操作却未能充分利用 GPU 核心。固定的计算图对简单和复杂输入的处理方式相同,浪费了不必要的计算资源。
本节探讨四种互补的架构效率方法:硬件感知设计原则在模型开发过程中主动整合部署约束,稀疏性利用技术加速修剪模型的计算,动态计算策略根据输入复杂性调整工作负载,以及操作融合方法通过组合操作减少内存流量。这些技术将算法优化转化为实际的性能提升。
硬件感知设计
硬件感知设计将目标平台的约束(如内存带宽、处理能力、并行能力和能量预算)直接纳入模型架构决策中。这种方法确保计算模式、内存访问和操作类型与硬件能力相匹配,从而最大化效率,适应各种部署平台。
高效设计原则
为了实现硬件效率,机器学习模型的设计需要在保证强大预测性能的同时,构建考虑计算成本、内存使用、推理延迟和功耗的架构。与训练后优化不同,硬件感知模型设计在一开始就主动整合硬件考虑因素。这确保了模型在各种硬件环境中都是计算高效的,并且可部署性强。
在这一主动方法中,充分利用特定硬件平台(如 GPU、TPU、移动或边缘设备)的优势,最大化并行性,优化内存层次结构,并通过硬件优化操作最小化延迟。表 10 总结的硬件感知模型设计原则,针对计算和系统约束的核心方面。
| 原则 | 目标 | 示例网络 |
|---|---|---|
| 缩放优化 | 调整模型深度、宽度和分辨率,以平衡效率和硬件约束。 | EfficientNet、RegNet |
| 计算减少 | 最小化冗余操作以降低计算成本,利用硬件特定的优化(如在移动芯片上使用深度可分离卷积)。 | MobileNet、ResNeXt |
| 内存优化 | 通过减少激活和参数存储需求,确保高效的内存使用,利用硬件特定的内存层次结构(如 GPU 中的本地和全局内存)。 | DenseNet、SqueezeNet |
| 硬件感知设计 | 针对特定硬件约束(如低功耗、并行性、高吞吐量)优化架构。 | 针对 TPU 优化的模型、MobileNet |
@tbl-hardware-efficient-design 中的原则协同作用:缩放优化使模型适应可用资源,计算减少通过深度可分离卷积等技术消除冗余操作,内存优化使访问模式与硬件层次结构对齐,硬件感知设计确保架构决策与平台能力匹配。综合运用这些原则,可以在保持准确性的同时,实现高效的模型。
缩放优化
模型架构的缩放涉及在深度、宽度和输入分辨率之间取得平衡,以优化与目标硬件的契合度。模型的每个组成部分,无论是深度、宽度还是输入分辨率,都会影响其资源消耗。在硬件感知设计中,这些维度不仅要针对精度进行优化,还要考虑到内存使用、处理能力和能量消耗,特别是在模型部署在特定硬件(如 GPU、TPU 或边缘设备)上时。
从硬件感知的角度来看,不同硬件平台(如 GPU、TPU 或边缘设备)与缩放维度的交互是重要的考虑因素。例如,尽管更深的模型能够捕捉更复杂的特征,但过大的深度会导致推理延迟增加、训练时间延长和内存消耗增加,这在资源受限的平台上尤其成问题。类似地,增加模型的宽度以处理更多的并行信息可能对具有高并行性的 GPU 和 TPU 有利,但也会增加内存使用的管理难度。输入分辨率的提高可以为图像分类等任务提供更精细的细节,但其计算成本呈指数级增长,可能会超出边缘设备的硬件内存或导致功耗效率降低。
从数学上讲,卷积模型的总 FLOP 数可以近似为: $$ \text{FLOPs} \propto d \cdot w^2 \cdot r^2, $$ 其中 $d$ 是深度,$w$ 是宽度,$r$ 是输入分辨率。在不考虑硬件限制的情况下,盲目增加这三个维度可能导致性能不佳,特别是在计算能力或内存带宽有限的设备上。
因此,高效的模型缩放需要平衡地管理这些参数,确保模型在硬件能力范围内运行,同时实现最佳性能。这就是复合缩放(compound scaling)发挥作用的地方。复合缩放并不是独立地调整深度、宽度和分辨率,而是通过相对于基准模型应用固定比例因子 $(\alpha, \beta, \gamma)$ 来平衡所有三个维度: $$ d = \alpha^\phi d_0, \quad w = \beta^\phi w_0, \quad r = \gamma^\phi r_0 $$ 这里,$\phi$ 是缩放系数,$\alpha$、$\beta$ 和 $\gamma$ 是根据硬件约束和经验数据确定的缩放因子。这种方法确保模型在增长时优化硬件资源的使用,使其在提高精度的同时保持高效。
例如,采用复合缩放的 EfficientNet 通过合理平衡深度、宽度和分辨率,展示了在计算效率和高性能之间的良好平衡。复合缩放在保持精度的同时降低了计算成本,是硬件感知模型设计中的一个关键考虑因素。这一方法对于在 GPU 或 TPU 上部署模型时尤为有效,因为可以充分利用其并行处理能力,但同时也需要谨慎管理内存和功耗。
计算减少
现代架构利用因式分解计算将复杂操作分解为更简单的组件,从而减少计算开销,同时保持表示能力。标准卷积在所有空间位置和通道上均匀应用滤波器,这在资源受限的硬件上形成了计算瓶颈。因式分解技术通过重构操作来解决这一低效问题,最小化冗余计算。
深度可分离卷积(depthwise separable convolutions)是 MobileNet 中提出的典型例子,它将标准卷积分解为两个阶段:深度卷积(对每个输入通道独立应用滤波器)和逐点卷积(1×1 卷积在通道间混合输出)。标准卷积在输入大小为 $h \times w$、输入通道数为 $C_{\text{in}}$、输出通道数为 $C_{\text{out}}$、卷积核大小为 $k$ 时的计算复杂度为:
$$ \mathcal{O}(h w C_{\text{in}} C_{\text{out}} k^2) $$
深度可分离卷积将其减少为:
$$ \mathcal{O}(h w C_{\text{in}} k^2) + \mathcal{O}(h w C_{\text{in}} C_{\text{out}}) $$ 通过消除通道混合操作中的 $k^2$ 因子,实现 5×-10× 的 FLOP 减少。这直接转化为移动和边缘设备上内存带宽需求的降低和推理延迟的改善。
其他互补的因式分解技术也扩展了这些好处。分组卷积(ResNeXt)将特征图划分为独立的组,分别处理后再合并,保持精度的同时减少冗余操作。瓶颈层(ResNet)在计算密集型操作之前,通过 1×1 卷积减少特征维度,将计算集中在最有价值的地方。结合稀疏性和硬件感知调度,这些技术最大化了在 GPU、TPU 和专用边缘处理器上的加速器利用率。
内存优化
内存优化27 主要解决在资源受限设备上,激活值、特征图和参数的内存需求超出硬件容量时带来的性能瓶颈。现代模型架构采用多种高效策略,既降低存储需求,又保证性能表现,从而确保在 GPU、TPU 和边缘 AI 平台上的可计算性与能效。
特征复用是 DenseNet 等架构采用的高效内存优化技术。传统卷积网络每层都会计算新的特征图,导致内存占用线性增长。而 DenseNet 通过复用前面各层的特征图,并有选择地进行变换,显著减少了需存储的特征图总数,从而降低内存需求且不损失精度。对于 $L$ 层网络,每层产生 $k$ 个新特征图,标准卷积网络需存储的特征图总数为: $$ \mathcal{O}(L k) $$
DenseNet 通过特征复用,减少了需存储的特征图数量,提升了参数效率,降低了内存占用,非常适合内存受限的硬件环境。
激活检查点(activation checkpointing)28 是训练阶段常用的另一种内存优化技术。标准反向传播需存储所有前向激活值,导致大模型训练时内存压力极大。激活检查点技术只保存部分激活值,其他激活在反向传播时动态重算,从而大幅降低内存消耗。
若需存储 $A_{\text{total}}$ 个激活,标准反向传播需全部保存: $$ \mathcal{O}(A_{\text{total}}) $$
采用激活检查点后,仅需保存一部分,其余动态重算,内存需求降为: $$ \mathcal{O}\Big(\sqrt{A_{\text{total}}}\Big) $$
特征复用和激活检查点能显著降低峰值内存消耗,尤其适合在有限显存下训练大模型。
参数量减少也是内存优化的重要手段,尤其针对大卷积核模型。例如 SqueezeNet 采用 $1\times 1$ 卷积先降维,再用标准卷积,极大减少参数量且不损失表达能力。标准卷积层参数量为: $$ \mathcal{O}(C_{\text{in}} C_{\text{out}} k^2) $$
通过 $1\times 1$ 卷积先降维,SqueezeNet29 将参数量降至 AlexNet 的 1/50,性能相当。该方法对边缘设备尤为重要。
特征复用、激活检查点和参数量减少是硬件感知模型设计的核心,使模型能适配现代加速器的内存限制,并通过减少内存访问降低功耗。TPU、GPU 等专用加速器通过多级缓存和高带宽内存高效处理稀疏或低内存模型,实现更快推理且开销极小。
自适应计算方法
动态计算让模型可根据输入复杂度自适应分配计算资源,优于传统固定结构模型。传统模型对所有输入一视同仁,简单样本也全流程处理,浪费算力且能耗高。动态计算则可对简单输入跳过部分层或操作,对复杂输入则深入处理。
这种自适应方式优化了计算效率、降低能耗、缩短延迟,同时保持预测性能。对于移动、嵌入式、自动驾驶等对实时性和能效要求极高的场景,动态计算尤为关键。
动态方案
动态方案允许模型在输入简单时有选择地减少计算,既节省资源又保持精度。以下介绍的早退架构等方法,展示了如何高效实现自适应计算。
早退架构(Early Exit)
早退架构允许模型在网络中间层即可输出预测,无需每次都完整前向推理。该方法特别适合实时和能效推理场景,可根据输入复杂度选择性地提前终止计算。
早退架构的核心机制是在网络中嵌入多个出口点。对于简单输入,模型在中间层即可高置信度分类,提前退出,减少不必要的计算;复杂输入则继续深入处理,确保精度。
典型代表是 BranchyNet30,在网络多处设置出口点。每个输入在中间层预测时,若置信度超过阈值则直接输出,否则继续后续计算。这样可在不影响复杂样本精度的前提下,大幅降低平均推理时间。
多出口视觉 Transformer 也是早退思想在 Transformer 架构上的扩展。通过在不同层插入轻量分类器,输入若能提前高置信度分类则直接输出,复杂样本则继续处理。该技术显著降低推理延迟,同时保证复杂样本的稳健性。
早退模型对移动端、边缘加速器等资源受限设备尤为有利。通过动态调整计算量,降低功耗和延迟,非常适合实时决策场景。
在 GPU、TPU 等硬件加速器上,早退架构还可通过并行评估不同出口路径进一步提升吞吐量。如下图(图 26)所示,每个 Transformer 层后都可接分类器和早退机制,根据置信度或延迟 - 精度权衡(LTE)动态决定是否提前退出,实现计算资源的动态分配。

条件计算(Conditional Computation)
条件计算指神经网络可根据输入动态决定激活哪些部分,从而减少不必要的计算。与早退架构只在置信度达标时提前退出不同,条件计算通过门控或动态路由机制,按需激活或跳过部分层、单元或路径,让模型将算力集中在最需要的地方。
如 SkipNet 采用门控机制,在输入简单时跳过部分 CNN 层。门控由轻量分类器预测是否跳过,复杂输入则全流程处理,兼顾速度与精度。
动态路由网络(如 Capsule Network)则通过路由机制动态选择信息流路径,复杂输入走更深路径,简单输入走浅层,显著减少运算量。
这些策略在实际应用中极具价值。例如自动驾驶场景,输入复杂度变化大,简单场景可走轻量路径,复杂场景则充分利用模型能力。条件计算确保系统能根据实时输入复杂度自适应分配算力,提升速度与能效。
基于门控的计算(Gate-Based Computation)
门控条件计算通过学习得到的门控机制,动态控制网络哪些部分被激活。与静态结构不同,门控机制可在推理时根据输入复杂度自适应激活子网络或层。
门控通常用二值或连续门控函数实现,轻量控制模块(如路由器)预测每层或路径是否执行。以 Dynamic Filter Network(DFN)为例,输入依赖性地选择卷积核,避免对所有输入一视同仁地应用全部滤波器。
Mixture of Experts(MoE)架构也是典型代表。门控网络为每个输入选择一小部分专家子网络参与计算,大幅提升模型容量而不增加推理成本。Google Switch Transformer 就是将专家机制引入 Transformer 的代表。

如上图(图 27),Switch Transformer 用路由器为每个 token 选择专家,极大提升参数规模但推理成本基本不变。
门控条件计算在多任务和迁移学习场景尤为有效,可实现任务间的自适应专业化。缺点是架构复杂度提升,门控和路由本身也有一定开销,部署到 GPU、TPU、边缘设备时需优化调度和批处理。
自适应推理(Adaptive Inference)
自适应推理指模型可在推理过程中根据输入复杂度动态调整计算深度和资源分配。与早退或层跳过不同,自适应推理可连续调节计算量,无需固定阈值。
如 Fast Neural Networks(FNNs)可根据实时复杂度估计动态激活部分层,简单输入只用浅层,复杂输入逐步加深。动态层缩放(dynamic layer scaling)则根据不确定性逐步增加计算深度,适合细粒度分类任务。
自适应推理特别适合对延迟敏感、资源动态变化的场景,如自动驾驶中简单车道检测只需少量计算,复杂多目标跟踪则需更多算力。GPU、TPU 等加速器可通过动态分配工作负载,最大化吞吐量并降低能耗。
实现挑战
动态计算虽带来灵活性和效率,但也引入了训练、推理效率、硬件执行、泛化和评估等多方面挑战。
训练与优化难点
动态计算需额外的控制机制(如门控网络、置信度估计、专家选择),这些决策多为离散型,难以用标准反向传播优化,常需强化学习或连续近似,增加训练成本且收敛慢。
不同输入走不同路径,导致梯度更新不一致,训练不稳定。门控阈值等超参数选择也更复杂,需精细调优以平衡精度与效率。
开销与延迟波动
动态计算虽减少了部分运算,但决策本身也有开销,尤其在资源受限环境下影响更大。更大的挑战是推理延迟的不确定性,部分输入推理极快,部分则较慢,难以满足严格实时性要求。
硬件执行低效
GPU、TPU 等现代加速器最擅长大批量、统一并行计算。动态计算引入条件分支,导致部分处理单元空闲,降低硬件利用率。内存访问模式也变得不规则,增加延迟。需专门的调度和编译优化,增加部署复杂度。
泛化与稳健性
动态计算可能导致部分输入分配的计算资源不足,出现偏置。门控设计不当还可能导致对训练路径过拟合,泛化能力下降。动态模型也更易受对抗攻击,攻击者可操控门控机制,迫使模型走错误路径。
评估与基准难题
主流 ML 基准假设固定计算预算,难以评估动态模型的真实效率。推理路径依赖输入,导致可复现性差,标准 FLOPs、延迟等指标难以反映动态架构的真实权衡。需新的评测方法。
尽管如此,动态计算仍是提升 ML 系统效率的前沿方向。未来需更稳健的训练技术、硬件感知执行策略和更完善的评测框架,才能充分释放其潜力。
稀疏性利用
稀疏性指张量(如权重矩阵、激活张量)中大量元素为零或近零。形式化定义为,对于 $T \in \mathbb{R}^{m \times n}$,稀疏度 $S$ 为: $$ S = \frac{\Vert \mathbf{1}{{T{ij} = 0}} \Vert_0}{m \times n} $$ 其中 $\mathbf{1}{{T{ij} = 0}}$ 为指示函数,$\Vert \cdot \Vert_0$ 为 L0 范数。
实际中常用近零阈值 $\epsilon$: $$ S_{\epsilon} = \frac{\Vert \mathbf{1}{{|T{ij}| < \epsilon}} \Vert_0}{m \times n} $$
稀疏性可自然产生(如正则化),也可通过剪枝等方法强制实现。高效利用稀疏性可大幅提升计算效率、节省内存和降低功耗,尤其适合移动、嵌入式和边缘设备。
稀疏类型
神经网络稀疏性分为非结构化稀疏和结构化稀疏。
非结构化稀疏是指单个权重被置零,无固定模式,常通过剪枝实现。灵活性高,但硬件利用率低,需专用优化。
结构化稀疏则按滤波器、神经元、通道等整体移除,便于 GPU、TPU 等硬件高效加速,适合对计算资源有严格要求的场景。
稀疏利用方法
高效利用稀疏性需专用技术和硬件支持。剪枝通过移除不重要权重(非结构化)或滤波器/通道/层(结构化)引入稀疏。结构化剪枝更易被硬件加速。
稀疏矩阵运算可跳过零元素,显著减少乘法次数。例如,稠密 $4\times 4$ 矩阵与向量相乘需 16 次乘法,稀疏实现仅需 6 次:
$$\left[\begin{array}{cccc}2 & 0 & 0 & 1 \\0 & 3 & 0 & 0 \\4 & 0 & 5 & 0 \\0 & 0 & 0 & 6\end{array}\right]\left[\begin{array}{c}x_1 \\x_2 \\x_3 \\x_4\end{array}\right]=\left[\begin{array}{c}2x_1 + x_4 \\3x_2 \\4x_1 + 5x_3 \\6x_4\end{array}\right]$$
低秩近似也是稀疏利用的重要方法。通过将大矩阵分解为更小的低秩矩阵(如 SVD),既保留主要信息,又大幅减少参数和计算量。推荐系统、NLP 等领域广泛采用。
此外,稀疏感知训练(如稀疏梯度下降)可在训练阶段直接学习稀疏表示,进一步提升效率。
稀疏硬件支持
理论上稀疏性可降低计算和内存,但实际加速需硬件/软件协同。CPU 对稀疏矩阵支持有限,GPU、TPU、FPGA 等加速器则需结构化稀疏才能高效利用。专用加速器需能高效处理稀疏数据,才能将理论压缩转化为实际加速。
如 MegaBlocks 将稀疏专家模型训练转化为块稀疏操作,开发了高效的 GPU 内核,提升了硬件利用率。
结构化稀疏模式
常见稀疏格式有块稀疏和 N:M 稀疏。块稀疏将大矩阵分为稠密子块,仅存储非零块,便于高效运算和存储。N:M 稀疏则在每 M 个元素中仅保留 N 个非零,其余为零,便于硬件优化。如下图(图 28、29)所示,NVIDIA cuSPARSE 支持块稀疏,A100 GPU 支持 2:4 稀疏。

N:M 稀疏则在每组 M 个元素中仅 N 个非零,便于硬件高效加速。如下图所示,2:4 稀疏在矩阵乘法中大幅提升效率。

GPU 与稀疏运算
GPU 擅长大规模并行计算,现代架构(如 NVIDIA Ampere)内置 Sparse Tensor Core,可自动跳过稀疏矩阵中的零元素,结构化剪枝效果尤佳。充分利用稀疏性可将矩阵乘法加速 2 倍以上,降低推理延迟和功耗。
但要充分发挥 GPU 稀疏加速能力,需稀疏结构与硬件架构匹配,结构化稀疏更易优化。
TPU 与稀疏优化
TPU 专为高效张量计算设计,内置稀疏权重支持,适合大规模 Transformer(如 BERT、GPT)。TPU 通过减少零元素计算负载,实现更快推理和更高能效。其高吞吐、低延迟的矩阵乘法单元可直接处理稀疏矩阵,适合剪枝和低秩近似模型。
FPGA 与稀疏计算
FPGA 可高度定制,适合需要精细控制的稀疏运算。可针对特定应用优化数据通路和内存管理,实现低延迟、高性能的稀疏矩阵运算,适合非结构化剪枝或自定义稀疏模式。
内存与能耗优化
稀疏网络可减少内存带宽压力,硬件加速器(详见 第 11 章:AI 加速 )通过跳过零值优化内存访问,提升能效。GPU、TPU 通过高带宽内存和稀疏感知访问模式,进一步降低能耗。
稀疏操作减少计算和内存访问,直接带来能耗降低31,尤其适合边缘和低功耗场景(详见 第 14 章:设备端学习 )。
未来:硬件与稀疏网络
未来硬件将更深度集成稀疏感知训练与优化算法,进一步降低计算和内存成本。类脑计算等新兴领域也为高效稀疏网络提供新思路。硬件与算法协同创新,将推动高效、可扩展 AI 在实时和低功耗场景的落地,助力 第 18 章:可持续 AI 。
挑战与局限
稀疏性虽能大幅降低计算和内存,但实际落地仍有诸多挑战。下表(表 11)总结了稀疏优化的主要难点。
| 挑战 | 描述 | 影响 |
|---|---|---|
| 非结构化稀疏优化 | 稀疏模式不规则,硬件难以高效利用稀疏性。 | 硬件加速有限,计算节省效果打折。 |
| 算法复杂度 | 剪枝和稀疏矩阵运算需复杂算法,尤其大模型更明显。 | 算法开销高,难以大规模应用。 |
| 硬件支持 | 加速器多针对结构化稀疏优化,非结构化稀疏难以高效利用。 | 硬件利用率低,性能提升有限。 |
| 精度权衡 | 过度稀疏会损失模型精度,需精细平衡。 | 性能下降风险,需大量调优和验证。 |
| 能效问题 | 稀疏存储和管理开销可能抵消计算节省带来的能耗优势。 | 若管理开销过大,能耗未必降低。 |
| 适用性有限 | 并非所有模型/任务都适合稀疏,部分领域需稠密表达。 | 并非所有模型/硬件都能从稀疏中获益。 |
非结构化稀疏的最大难点在于硬件利用率低。剪枝后权重分布不规则,GPU、TPU 等加速器难以高效跳过零元素,理论加速难以落地。结构化稀疏则更易被硬件优化。
算法复杂度也是一大挑战。非结构化剪枝需复杂的权重重要性评估,稀疏矩阵运算也需专用算法,尤其大模型下开销更大。
硬件支持有限,尤其是非结构化稀疏。即便硬件支持稀疏操作,稀疏存储和管理的额外开销也可能抵消节能优势。
稀疏性与精度间需精细权衡,过度稀疏易导致欠拟合。部分任务(如图像分割、强化学习)对稀疏性收益有限。
组合优化
稀疏性与剪枝、量化、高效模型设计等其他优化手段结合,能进一步提升效率。
稀疏与剪枝
剪枝后模型通常变稀疏,但稀疏模式(结构化/非结构化)决定了硬件优化效果。结构化剪枝(如滤波器/层剪枝)更易被硬件加速,非结构化剪枝则难以充分利用。
稀疏与量化
稀疏与量化结合可极大降低内存和计算,但非结构化稀疏加剧低精度权重处理难度。GPU、TPU 在低精度下可进一步加速稀疏矩阵运算,CPU 则难以兼顾。
稀疏与模型设计
高效模型设计(如深度可分离卷积、低秩近似、动态计算)本身已优化结构,稀疏性可进一步提升效率。但需硬件支持,否则难以发挥稀疏优势。
稀疏与优化挑战
多技术协同需精细管理精度权衡。GPU、TPU 等加速器对结构化稀疏优化良好,但对非结构化稀疏或稀疏 - 量化组合支持有限。需结合硬件能力,合理选择技术组合,平衡精度、计算、内存和硬件效率。
实施策略与评估
本节聚焦于系统性落地方法。单一技术往往难以独立奏效,生产系统需多技术协同优化,平衡多重约束。高效部署需结构化的系统分析、优化效果评估和多技术集成。
本节将指导如何从理论走向实践,聚焦三个关键问题:优化应聚焦何处?如何衡量优化效果?如何多技术协同避免冲突和收益递减?
分析与机会挖掘
优化的基础是系统分析,识别算力消耗和优化潜力最大的环节。首先需判断模型优化是否真的能提升系统性能,因为在生产环境中,模型计算往往只占总开销的一部分。
现代 ML 模型资源消耗高度异构,部分层、操作或数据路径占用大部分内存、算力或延迟。理解这些模式有助于优化聚焦,最大化收益且最小化精度损失。
高效分析需先建立全方位基线,包括静态内存(参数、缓冲区)、动态内存分配、算力(FLOPS、实际执行时间)、能耗(尤其边缘/电池场景)和延迟(端到端响应、关键路径)。如用 PyTorch Profiler 分析 ViT 部署,发现注意力层占 65% FLOPs(适合结构化剪枝)、LayerNorm 占 8% 延迟但仅 2% FLOPs(内存瓶颈)、分类头占 1% 计算但 15% 参数内存。优化建议:优先对注意力层做幅值剪枝(高 FLOP 减少),分类头量化为 INT8(大内存节省,精度影响小),LayerNorm 融合优化(缓解内存带宽瓶颈)。
更进一步,需分析模型对不同类型修改的敏感性。并非所有参数对精度贡献相同,结构化敏感性分析可指导哪些部分可激进优化,哪些需保守处理。分层敏感性分析可揭示哪些组件对精度最关键,指导剪枝、量化等策略选择。
优化效果评估
优化需严谨的多维度评测框架,不能只看精度。需同时衡量精度保持、算力提升、内存减少、延迟改善和能耗节省等目标,平衡多目标、结构化决策。
评测框架应在优化前建立全面基线,包括精度(分类准确率、校准性、公平性、稳健性)、效率(FLOPS、内存带宽)、实际执行时间、峰值内存和能耗等。
如将 ResNet-50 从 FP32 量化为 INT8,基线为 Top-1 精度 76.1%、V100 延迟 4.2ms、模型 98MB、单次推理能耗 0.31J。量化后 Top-1 精度 75.8%(降 0.3%)、延迟 1.3ms(加速 3.2 倍)、模型 25MB(减小 3.9 倍)、能耗 0.08J(节能 3.9 倍)。进一步分析发现,细粒度类别精度下降 0.1%-1.2%,校准误差从 2.1% 升至 3.4%,GPU 上加速 3.2 倍,CPU 上仅 1.8 倍,说明收益依赖硬件。
有了全面基线后,需系统跟踪优化影响。多技术协同时,需理解不同方法的交互,顺序应用可能带来复合收益,也可能出现收益递减或冲突。
多技术集成策略
最大化优化收益需跨三维框架集成多种技术。模型表示(剪枝)减少参数,数值精度(量化)降低单次运算成本,架构效率(操作融合、动态计算)减少执行开销。三者协同,带来乘法级收益。
应用顺序至关重要。例如将 BERT-Base 部署到移动端,第一步结构化剪枝去除 30% 注意力头和 40% FFN 维度,参数降 75%,精度从 76.2% 降至 75.1%;第二步知识蒸馏恢复至 75.9%;第三步量化感知训练(INT8)再降 4 倍内存,最终精度 75.6%。整体内存降 16 倍(440MB→28MB),移动 CPU 推理加速 12 倍,最终精度损失仅 0.6%(若先量化再剪枝则损失 2.1%)。
该案例说明顺序的重要性:先剪枝可将重要权重集中,后续量化更有效。若先量化再剪枝,重要性排序受精度影响,最终精度更低。高效集成需理解依赖关系,合理设计应用顺序,最大化复合收益。现代 AutoML 方法也在利用三维框架自动发现最优组合。
AutoML 与自动化优化策略
随着机器学习模型日益复杂,实际部署时需在精度、效率和硬件约束等多重因素间权衡。前文已介绍了剪枝、量化、神经架构搜索等多种优化技术,各自针对模型效率的不同方面。然而,如何高效应用这些优化,往往需要大量人工经验、领域知识和反复试验。
自动化机器学习(AutoML)旨在简化这一过程,借助机器学习算法自动搜索最优模型配置,继承自 第 8 章:AI 训练 的训练方法论。AutoML 框架通过自动优化架构、超参数、模型压缩策略等关键参数,减少人工干预。系统性探索庞大的模型设计空间,AutoML 能在保持精度的同时提升效率,常常发现人工调优难以覆盖的新颖方案。
AutoML 并非取代专家,而是为模型优化提供结构化、可扩展的自动化工具。如 图 30 所示,AutoML 与传统流程的最大区别在于其自动化了预处理、训练和评估等环节。开发者只需设定高层目标(如延迟、内存、精度约束),AutoML 系统便能自动探索满足这些约束的最优配置,助力 第 16 章:稳健 AI 中的高稳健性部署策略。

本节将系统介绍 AutoML 的核心优化维度、主流方法论及其挑战与局限,揭示 AutoML 如何作为集成框架统一前述多种优化策略。
AutoML 优化维度
AutoML 旨在多维度优化机器学习模型,兼顾效率、精度与可部署性。与传统方法只关注单一技术(如量化或剪枝)不同,AutoML 采用整体视角,联合考虑多种因素,系统性搜索最优模型配置,实现理论与实际部署的平衡。
AutoML 的首要优化目标之一是神经网络架构搜索(NAS)。高效架构设计需在层结构、连接模式、计算成本间权衡。NAS 通过结构化探索不同网络结构,评估效率,自动选出最优设计。MobileNetV3、EfficientNet 等高效架构即由 NAS 自动发现,超越了人工设计。
除架构设计外,AutoML 还聚焦超参数优化32,如学习率、批量大小33、权重衰减、激活函数等,这些参数对模型性能影响极大。
AutoML 框架采用贝叶斯优化34、进化算法、自适应启发式等结构化搜索策略,远优于人工试错。
AutoML 还自动化模型压缩,如剪枝、量化等,降低模型内存和计算需求,适合资源受限硬件。AutoML 框架自动选择剪枝阈值、稀疏模式、量化位宽,优化模型速度与能效,尤其适合边缘 AI 场景。
最后,AutoML 关注部署感知优化,确保最终模型适配实际硬件。不同平台对内存带宽、计算吞吐、能效等有不同约束,AutoML 框架集成硬件感知优化,自动调整计算负载、内存访问和执行策略。
多维度优化让 AutoML 成为统一的模型效率提升平台,既保证理论最优,也确保实际部署可行,适配多样化应用和硬件。
优化策略
AutoML 系统通过系统性探索不同配置,自动寻找架构、超参数和压缩策略的最优组合。与依赖专家经验的人工调优不同,AutoML 利用算法搜索高维设计空间,兼顾精度、效率和部署约束。
NAS 是 AutoML 的基础,通过强化学习、进化算法、梯度优化等自动化架构设计。系统性评估候选架构,发现超越人工设计的结构。超参数优化(HPO)则用贝叶斯优化、自适应启发式等方法高效调优训练参数,远快于网格搜索。
模型压缩优化自动选择剪枝、量化策略,结合部署需求权衡模型体积、延迟和精度,便于在 第 14 章:设备端学习 等场景高效部署。数据处理策略如自动特征选择、自适应增强、数据集均衡等进一步提升稳健性(见 第 16 章:稳健 AI ),且无额外计算负担。
元学习(Meta-learning)是 AutoML 的新进展,通过迁移历史优化经验,加速新任务的搜索。AutoML 系统可智能探索空间,降低训练和评估成本,加快新任务适应。
许多现代 AutoML 框架已实现端到端自动化,将架构搜索、超参数调优、模型压缩集成到单一流水线。Google AutoML、Amazon SageMaker Autopilot、Microsoft Azure AutoML 等平台提供全自动工作流,极大简化模型优化流程。
这些策略的集成让 AutoML 成为可扩展、高效的模型优化方案,减少人工试验,加速开发,发现人工难以覆盖的新型架构和配置,支持 第 12 章:AI 基准测试 的结构化评测。
AutoML 优化挑战
AutoML 虽为模型优化提供了强大框架,但也带来一系列挑战与权衡。其效果受限于计算资源、数据集特性和具体应用约束。
最大挑战之一是计算成本。搜索最优架构、超参数和压缩策略需评估大量候选模型,每个都需训练和验证。NAS 等方法尤其昂贵,常需数千 GPU 小时。早停、权重共享、代理模型等可降低成本,但对算力有限的团队仍是主要瓶颈。
另一个挑战是搜索策略偏置,可能影响最终模型选择。AutoML 的优化过程受启发式和目标函数引导,若搜索空间设计不当,可能遗漏更优结构或参数。训练数据的偏差也可能在 AutoML 流程中被放大,影响最终模型。
泛化与可迁移性也是难题。AutoML 生成的模型针对特定数据和部署条件优化,迁移到新任务或环境时性能可能下降。与人工设计模型可凭经验选取泛化性强的结构不同,AutoML 依赖于受限空间内的经验评估,稳健性存疑。
可解释性也是重要考量。许多 AutoML 生成的架构和配置虽高效,但缺乏透明度,难以理解其为何有效,给调试和定制带来困难。部分 AutoML 技术的“黑箱”特性限制了人类对优化过程的洞察。
此外,自动化与可控性间也需权衡。AutoML 虽减少了人工干预,但也屏蔽了许多决策细节,专家难以针对特定应用微调。部分场景下,领域知识对模型优化至关重要,完全自动化未必能覆盖所有约束。
尽管如此,AutoML 仍在不断进化,研究聚焦于降低计算成本、提升泛化性和增强可解释性。随着这些改进,AutoML 有望在高效模型开发中扮演更重要角色,让 AI 系统更易用、更高效。
本章介绍的优化技术——涵盖模型表示、数值精度、架构效率和自动化选择——构成了高效 ML 系统的完整工具箱。但实际落地还需强大的软件基础设施,将优化研究与生产部署通过易用 API、高效实现和无缝集成连接起来。
实现工具与软件框架
理解剪枝、量化、高效数值等优化技术的理论很重要,但实际应用高度依赖于健全的软件支持。没有完善的框架和工具,这些优化方法难以落地。手动实现量化需修改模型定义、插入量化操作,剪枝需直接操作权重张量,模型规模一大实现难度激增。
现代 ML 框架提供高级 API 和自动化工作流,极大简化了优化技术的应用。框架解决了关键难题:内置常用优化模块、辅助超参数调优(如剪枝计划、量化位宽)、通过自动评估管理精度 - 压缩权衡,并通过设备特定代码生成确保硬件兼容。
这些软件基础设施将理论优化方法转化为可直接应用于生产的工具(见 第 13 章:机器学习运维 )。生产优化还需考虑模型版本管理、优化对数据流水线的影响、开发与部署环境间的优化工件管理、优化失败时的回滚机制等。这些能力让高效模型大规模落地成为可能,打通了学术与工业的鸿沟。
模型优化 API 与工具
TensorFlow、PyTorch、MXNet 等主流框架均提供丰富的优化 API,使开发者无需从零实现复杂算法即可应用优化技术(见 第 7 章:AI 框架 )。这些内置优化提升了模型效率,并确保最佳实践。
TensorFlow Model Optimization Toolkit 支持量化、剪枝、聚类。QAT 可将浮点模型系统性转换为低精度(INT8),权重和激活均可量化,适配多种架构。剪枝算法可按不同粒度(单权重到整层)引入稀疏性,便于针对需求定制。权重聚类则通过聚合相似权重实现压缩,兼顾功能和效率。
PyTorch 也内置了量化和剪枝模块。torch.quantization 提供模型低精度转换工具,支持后训练量化和量化感知训练,如下例所示:
import torch
from torch.quantization import QuantStub, DeQuantStub, prepare_qat
# 定义支持量化的模型
class QuantizedModel(torch.nn.Module):
def __init__(self):
super().__init__()
self.quant = QuantStub()
self.conv = torch.nn.Conv2d(3, 64, 3)
self.dequant = DeQuantStub()
def forward(self, x):
x = self.quant(x)
x = self.conv(x)
return self.dequant(x)
# 准备量化感知训练
model = QuantizedModel()
model.qconfig = torch.quantization.get_default_qat_qconfig()
model_prepared = prepare_qat(model)
剪枝方面,PyTorch 的 torch.nn.utils.prune 支持非结构化和结构化剪枝,示例如下:
import torch.nn.utils.prune as prune
# 非结构化剪枝
module = torch.nn.Linear(10, 10)
prune.l1_unstructured(module, name="weight", amount=0.3)
# 剪除 30% 权重
# 结构化剪枝
prune.ln_structured(module, name="weight", amount=0.5, n=2, dim=0)
内置优化 API 的优势在于极大降低了实现复杂度,开发者可直接调用标准化接口,无需自行实现复杂算法,且适用于多种架构,保证了结果的可靠性和可复现性。
这些框架也是学术前沿与工程实践的桥梁。新优化技术一经研究社区提出,框架维护者便会集成到 API 中,让开发者无需自行实现即可用上最新方法。
内置 API 还便于快速实验和对比不同优化策略,帮助开发者高效探索最优配置,兼顾性能与资源约束。
随着模型优化技术不断演进,主流框架也在持续扩展内置支持,进一步降低高效模型部署门槛,推动高质量优化方法的标准化和普及。
硬件专用优化库
现代 ML 框架中的硬件优化库(详见 第 7 章:AI 框架 )支持在不同硬件平台高效部署优化模型。这些库与训练和部署流水线深度集成,为模型表示、数值精度、架构效率等多维优化提供硬件级加速。
如 TensorRT、XLA35、OpenVINO 等库为剪枝等模型表示优化提供稀疏感知加速,支持高效稀疏计算。TensorRT 针对结构化稀疏(如 2:4 剪枝)优化,TPU 通过 XLA 支持稀疏矩阵,FPGA 可用 Vitis AI 实现自定义稀疏执行。
知识蒸馏也可结合硬件感知优化,助力小模型高效推理。TensorRT、OpenVINO、SNPE 等库可对蒸馏模型做低功耗优化,常与量化、结构重组结合,满足硬件约束。NAS 发现的新架构可用 TVM36、TIMM 等编译器针对多硬件后端调优。
数值精度优化方面,这些库广泛支持 PTQ、QAT。TensorRT、TensorFlow Lite 在模型转换时实现 INT8/INT4 量化,利用专用硬件加速移动 SoC、边缘 AI 芯片。NVIDIA TensorRT 支持基于校准数据集的量化。
更细粒度的通道/分组量化在 SNPE、OpenVINO 等框架中支持。PyTorch、ONNX Runtime 支持动态量化,适应不同硬件条件。极端量化(如二值/三值)可用 CMSIS-NN 等库在 ARM Cortex-M 微控器高效执行。
架构效率技术与硬件执行框架深度集成。TensorFlow XLA、TVM 通过操作融合和内核重排提升 GPU、TPU、边缘设备效率。
稀疏感知执行已广泛支持多平台。NVIDIA GPU 利用稀疏张量核加速结构化稀疏模型,TPU 实现硬件级稀疏矩阵优化,FPGA 可用 Vitis AI 实现自定义稀疏计算。
硬件优化库与 ML 框架的深度集成,使开发者能高效实现剪枝、量化、NAS、动态计算、稀疏感知执行,并确保最优适配目标硬件,助力 第 13 章:机器学习运维 的部署策略。多维优化能力是高效部署 ML 模型的关键。
优化过程可视化
模型优化技术会改变结构和数值表示,但其影响难以直观理解。专用可视化工具帮助开发者洞察剪枝、量化等优化对模型行为的影响,如稀疏模式、量化误差分布、激活变化等。
量化效果可视化
量化降低数值精度,引入舍入误差,影响模型精度。可视化工具可直观展示误差分布,帮助诊断和缓解精度下降。
常用方法有量化误差直方图,显示权重和激活的误差分布,揭示误差是否呈高斯分布或有异常层。TensorFlow Quantization Debugger、PyTorch FX Graph Mode Quantization 等工具支持误差分析和方法对比。
激活可视化可检测低精度下的溢出问题。ONNX Runtime、NVIDIA TensorRT Inspector 等工具支持激活前后着色,便于发现饱和和截断问题,及时调整校准策略。如下图(图 31)为 AlexNet 卷积核的权重着色图。

此外,跟踪量化误差随训练过程的变化也很重要。QAT 期间监控均方量化误差(MSQE)有助于发现数值精度影响学习的关键点。TensorBoard、PyTorch 量化调试 API 支持实时跟踪,及时发现训练不稳定。
集成这些可视化工具,有助于早期发现和修正问题,确保优化模型兼顾精度与效率。可视化为理解稀疏、量化、架构优化对模型的影响提供了实证依据,指导高效模型压缩与部署。
稀疏模式可视化
稀疏可视化工具通过映射被剪除权重和稀疏分布,帮助分析剪枝对不同层的影响。TensorBoard(TensorFlow)、Netron(ONNX)等工具支持层级和权重级稀疏可视化。
常见方法有稀疏热力图,用颜色深浅表示各层被剪除权重比例,深色表示高稀疏度,如 图 32 所示。该方法让剪枝过程更透明,便于优化策略调整。
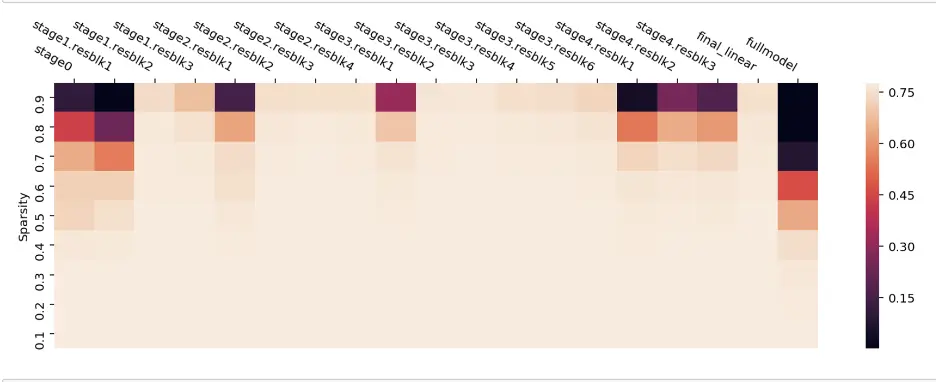
趋势图可跟踪多轮剪枝的稀疏度变化,揭示全局稀疏度的演化过程。TensorFlow Model Optimization Toolkit、SparseML 等工具支持逐层稀疏度跟踪,便于精细调优。
DeepSparse、PyTorch 剪枝工具等也支持生成上述可视化,帮助分析剪枝对模型各部分的影响。可视化让稀疏数据更直观,助力高效优化。
技术对比
深入探讨三大优化方法后,系统对比有助于理解各自的效率 - 精度权衡,指导实际部署选择。
| 技术 | 主要目标 | 精度影响 | 训练成本 | 硬件依赖 | 最佳应用场景 |
|---|---|---|---|---|---|
| 剪枝 | 降低 FLOPs/体积 | 中等 | 低(微调) | 高(需稀疏硬件) | 延迟敏感应用 |
| 量化 | 降低体积/延迟 | 低 | 低(PTQ)/高(QAT) | 高(需 INT8 支持) | 边缘/移动端部署 |
| 蒸馏 | 降低体积 | 低 - 中等 | 高(需重训练) | 低 | 需高质量小模型的场景 |
理解这些权衡有助于系统性选择技术(见表 12)。剪枝适合有稀疏计算硬件、需极致 FLOP 降低的场景;量化适配性最强,适合多样化部署;蒸馏虽训练成本高,但能稳定产出高质量压缩模型,适合对精度要求极高的场景。
这些技术可协同应用,常见顺序为:先剪枝降参数,再量化优化数值表示,最后通过蒸馏微调恢复精度。顺序应用可实现 10-50 倍压缩,精度损失极小,适配多种部署需求。
常见误区与陷阱
模型优化是 ML 系统中最复杂的领域之一,多技术协同才能兼顾效率与精度。剪枝、量化、蒸馏等技术的复杂依赖关系,易导致误用和次优结果,影响部署成败。
误区: 可独立应用多种优化技术,无需考虑相互影响。
这种误解导致团队同时应用多种优化,未考虑其交互。剪枝与激进量化叠加可能导致精度损失超标,蒸馏若以重度剪枝模型为教师,可能将次优行为传递给学生。不同优化方法间可能相互干扰,需系统性协调。
陷阱: 只关注理论指标,忽视实际部署性能。
许多团队只关注参数量、FLOPs、模型体积等理论指标,未测量实际部署性能。参数少的模型可能缓存局部性差、内存访问不规律,硬件利用率低,理论收益难以落地。量化虽减小模型体积,但在部分硬件上因格式转换反而增加推理延迟。优化需以实际部署指标为准。
误区: 激进量化不会显著影响模型性能。
这种观点导致团队盲目追求极端量化。多数模型可容忍中等量化,但极端量化易导致精度崩溃、数值不稳定或训练发散。不同架构和任务对量化敏感度不同,需具体分析,不能一概而论。部分操作如注意力、归一化层需高精度。
陷阱: 只用训练后优化,忽视训练感知方法。
为简化流程,团队常在训练后应用优化,但这通常不如训练感知方法(如 QAT、渐进剪枝、蒸馏集成)效果好。训练后优化虽方便,但结果往往不理想,难以满足部署需求。
陷阱: 只关注模型本身,忽视系统级性能瓶颈。
许多优化只关注模型复杂度,未分析系统整体。模型再高效,若数据预处理、I/O、网络通信占主导,整体延迟难降。内存带宽、缓存未命中、批处理低效等也会抵消模型优化收益。单模型推理优化可能错失批处理、并行、流水线等系统级机会。高效优化需系统分析,确保模型级提升能转化为系统级收益。这一系统视角与 第 13 章:机器学习运维 的运维原则直接相关,确保优化有助于整体可靠性和可维护性。
总结
模型优化是理论 ML 进步与实际部署之间的桥梁。实际部署需面对算力、内存、能效等多重约束,需精细工程。全章展示了精度与效率的核心张力,驱动了多维度优化技术的繁荣。现代优化不仅仅是减小模型体积或复杂度,更是系统性重组模型结构、数值精度和计算模式,在保留核心能力的同时极大提升效率。
本章提出的优化框架,展示了如何系统性地细化模型设计以适配部署约束。从 440MB 的 BERT-Base 到 28MB 的可部署版本,正是剪枝(结构压缩)、蒸馏(精度保持)、量化(极致压缩)协同的结果。硬件感知设计原则确保优化策略与底层计算架构对齐,最大化实际收益。
要点总结
- 模型优化需跨结构、精度、架构效率多维协同,BERT 通过剪枝、蒸馏、量化实现 16 倍压缩
- 硬件感知优化让模型特性与计算架构深度适配,最大化实际性能
- 自动化优化(AutoML)可发现超越人工的技术组合
- 优化需兼顾精度与部署约束,DistilBERT 以 40% 参数保留 97% 性能
- 没有万能方案,最优策略取决于具体部署、硬件和应用需求
AutoML 框架的出现标志着优化策略自动发现的范式转变。自动化方法基于训练方法论,指向自优化系统的前沿。系统性探索优化空间,常能发现超越人工的新型技术组合,实现更优的效率 - 精度权衡。随着模型规模和部署场景日益多样,掌握这些优化技术将成为连接研究精度与生产效率的关键能力。
测验:模型优化
测试你对机器学习模型优化技术的理解,包括剪枝、量化、知识蒸馏等核心概念
微控制器约束:Arduino Uno 仅有 2KB SRAM 和 32KB 闪存。ARM Cortex-M4 通常配备 256KB 闪存、64KB RAM,主频最高 168MHz,而现代 GPU 主频 3000+ MHz、内存 16-80GB,资源差距高达 1 万倍以上。 ↩︎
边缘 ML:指 ML 推理在本地设备(如手机、IoT 传感器、自动驾驶车辆)而非云端完成。可将 100-500ms 的云端延迟降至本地 <10ms,但模型规模受限于 10-500MB,而云端模型可达数 GB。 ↩︎
Tiny ML:超低功耗 ML 系统,功耗低于 1mW,内存小于 1MB。适用于助听器、智能传感器、可穿戴设备等“永远在线”场景。模型规模通常为 10-100KB,相比云端模型缩小 1 万倍。 ↩︎
内存带宽:现代 GPU(如 H100 SXM5)带宽达 3.0 TB/s,而高端移动 SoC 仅 25-50 GB/s。大语言模型训练需显存为模型体积的 1-2 倍(16GB 模型需 32GB+ 显存),形成“内存墙”瓶颈。 ↩︎
混合精度训练:前向用 FP16,反向梯度用 FP32,训练速度提升 1.5-2 倍,显存减半。NVIDIA AMP 可在 V100 上保持 FP32 精度,速度提升约 1.6 倍,A100 上可达 2.2 倍。 ↩︎
稀疏性:模型中零值参数的比例。90% 稀疏模型仅有 10% 非零权重,内存和计算量可降至 1/10(需专用硬件)。现代 Transformer 推理阶段激活稀疏度可达 80-95%。 ↩︎
矩阵分解:将大权重矩阵(如 4096×4096)分解为更小的矩阵(4096×256 × 256×4096),参数量从 1600 万降至 200 万(8 倍压缩)。SVD 低秩近似可保持 95%+ 精度,在移动端实现 3-5 倍加速。 ↩︎
LoRA(低秩适配):微调时冻结预训练权重,仅添加小型可训练矩阵,将可训练参数从 175B 降至约 120 万,训练内存和计算量降至 1/3,性能基本不变。 ↩︎
算子融合:图级优化,将多个操作合并为单一内核,内存带宽降低 30-50%。如 ResNet-50 中 Conv+BN+ReLU 融合在 V100 上加速 1.8 倍,BERT Transformer 块通过注意力融合延迟降低 25%。 ↩︎
梯度检查点:内存优化技术,通过反向传播时重算中间激活,换取内存节省。可使 Transformer 模型显存降低 20-50%,支持更大 batch 或模型。 ↩︎
ML 并行计算:高端数据中心 GPU 拥有 5000-10000+ 核心,CPU 仅 8-64 核。NVIDIA H100 张量性能 989 TFLOPS,Intel Xeon 3175-X 仅约 1.5 TFLOPS(双精度),ML 任务并行度高,GPU 性能密度高 650 倍。 ↩︎
帕累托前沿:优化中提升一项指标(如速度)必然牺牲另一项(如精度)。如 EfficientNet 系列在准确率-FLOPS 权衡上表现最优,B0(77.1%/390M FLOPs)到 B7(84.4%/37B FLOPs),规模越大收益递减。 ↩︎
TensorFlow 模型优化:官方 Toolkit 支持量化(模型体积缩小 4 倍)、剪枝(稀疏度最高 90%)、聚类等技术。YouTube、Gmail、Google Photos 等在全球 40 亿设备上部署模型均采用该工具。 ↩︎
结构化剪枝:ResNet-34 滤波器剪枝可将 FLOPs 降低 50%,CIFAR-10 精度仅降 1%。MobileNetV2 通道剪枝参数减少 73%,精度保留 96.5%,ARM 端推理加速 3.2 倍。 ↩︎
彩票假说:ResNet-18 剪枝后仅保留 10-20% 参数,CIFAR-10 精度 93.2%(全模型 94.1%);BERT-base 剪枝后参数减少 90%,性能保留 97%,收敛速度提升 5-8 倍。 ↩︎
ONNX 部署:ONNX Runtime 在 CPU 平台上相较 TensorFlow 提速 1.3-2.9 倍,相较 PyTorch 提速 1.1-1.7 倍。ResNet-50 推理延迟从 7.2ms 降至 2.8ms,BERT-Base 从 45ms 降至 23ms,得益于 ONNX Runtime 的图融合与内存池优化。 ↩︎
TensorRT 优化:NVIDIA TensorRT 推理速度最高可达 CPU 基线的 40 倍,V100 GPU 上常见优化提升为 5-8 倍。ResNet-50 INT8 推理仅需 1.2ms(FP32 为 4.8ms),BERT-Large 从 10.4ms 降至 2.1ms。层融合减少 80% 的 kernel 启动次数,内存带宽降低 50%。 ↩︎
BERT 压缩:BERT-Base(1.1 亿参数)可压缩至 6700 万参数(减少 39%),GLUE 分数仅下降 1.2%。剪枝可移除 192 个注意力头中的 144 个,几乎不影响性能,层剪枝将 12 层降至 6 层,仍保持 97.8% 的表现。 ↩︎
DistilBERT:以 40% 更少参数(6600 万 vs 1.1 亿)和 60% 更快推理速度,达到 BERT-Base 97% 的性能。SQuAD v1.1 上 DistilBERT F1 为 86.9,BERT 为 88.5,内存从 1.35GB 降至 0.54GB,延迟从 85ms 降至 34ms。 ↩︎
EfficientNet 剪枝:EfficientNet-B0 结构化剪枝 70% 后,ImageNet 精度仍有 75.8%(原始为 77.1%),在移动端加速 2.8 倍。通道剪枝将 FLOPs 从 3.9 亿降至 1.4 亿,Pixel 4 上推理低于 20ms。 ↩︎
Kullback-Leibler (KL) 散度:衡量概率分布差异的信息论指标。知识蒸馏中,KL 散度典型值为 0.1-2.0 nats,若大于 3.0 说明教师 - 学生匹配较差,需调整温度或模型结构。 ↩︎
交叉熵损失:分类任务常用损失函数,衡量预测分布与真实分布的差异。二分类时范围 0-∞(越低越好),大于 2.3 表示性能较差(低于随机猜测)。计算公式为 -log(预测的真实类别概率)。 ↩︎
温度参数:控制知识蒸馏中概率分布的平滑度。T=1 为标准 softmax,T=3-5 常用于蒸馏(揭示类别关系),T=20+ 时分布趋于均匀。最佳温度:CIFAR-10 用 T=3,ImageNet 用 T=4,BERT 等语言模型用 T=6。 ↩︎
硬件感知 NAS:MnasNet 在 315M FLOPs 下实现 78.1% ImageNet 精度,优于 MobileNetV2 的 72.0%(300M FLOPs)。EfficientNet-B0 以 390M FLOPs 达到 77.1% 精度,精度/FLOP 比 ResNet-50 高 23%,移动端推理快 4.9 倍。 ↩︎
NAS 评估指标:多目标优化综合考虑精度(top-1/top-5)、延迟(ms)、内存(MB)、能耗(mJ)。Pareto 最优架构效率提升 15-40%。 ↩︎
FBNet:ImageNet 精度 74.9%,FLOPs 375M,三星 S8 延迟 23ms,比 MobileNetV2 快 15%。延迟感知搜索基于设备实际性能测量。 ↩︎
内存优化:DenseNet-121 通过特征复用将激活内存消耗降至 ResNet-50 的一半,仅需 7.9MB(ResNet-50 为 15.3MB),适用于 ImageNet。MobileNetV3 采用深度可分离卷积,在 2GB 移动设备上实现 73% 内存节省。 ↩︎
激活检查点:通过仅保存部分激活值、其余在反向传播时重算,实现内存与计算的权衡。可使大规模 Transformer 训练内存降低 20-50%,训练时间仅增加 15-20%。GPT-3 等大模型训练离不开该技术。 ↩︎
SqueezeNet:DeepScale/Berkeley 提出的 fire 模块(squeeze+expand)结构,实现了 AlexNet 级别精度(ImageNet top-1 57.5%),参数量仅 1.25M(AlexNet 为 60M),模型体积从 240MB 降至 0.5MB,适合手机和嵌入式部署。 ↩︎
BranchyNet:率先提出多分支早退结构,在 CIFAR-10 上实现 2-5 倍加速,精度损失小于 1%。简单输入平均推理时间降至 20-40%,复杂输入仍走全流程,适合移动端实时处理。 ↩︎
稀疏能耗节省:BERT 90% 稀疏度在 V100 上训练能耗降 2.3 倍,推理能耗降 4.1 倍。A100 上 2:4 结构化稀疏节能 1.6 倍,精度保持 99%。TPU、GPU 等加速器已针对稀疏优化,稀疏网络更快且更节能。 ↩︎
超参数优化:仅学习率搜索即可提升模型精度 5-15%。4 个超参数各 10 个取值的网格搜索需 1 万次训练,贝叶斯优化可降至 100-200 次,节省数周计算。 ↩︎
批量大小影响:大批量(512-2048)可提升吞吐量 2-4 倍,但需梯度累积以适应内存。线性缩放法则:学习率随批量线性放大,使 ImageNet 训练可在 1 小时内完成(批量 8192)。 ↩︎
贝叶斯优化:用概率模型指导超参数搜索,建模目标函数不确定性。比随机搜索少 10-50 倍评估次数。GPyOpt、Optuna 等框架支持多目标贝叶斯优化,适合神经网络。 ↩︎
XLA(加速线性代数):Google 的领域专用编译器,通过操作融合和内存优化,使 ResNet-50 推理加速 1.15-1.4 倍,BERT-Large 训练加速 1.2-1.7 倍。HBM 流量减少 25-40%,TPU 能耗降低 15-30%。 ↩︎
TVM(Tensor 虚拟机):Apache TVM 自动调优使 ARM CPU 推理加速 1.2-2.8 倍,移动 GPU 加速 1.5-3.2 倍。图级优化使边缘设备推理延迟降 40-60%,得益于操作调度和内存规划。 ↩︎