DSP 频谱特征 | Jimmy Song

概述

与运动（或振动）相关的 TinyML 项目通常涉及来自 IMU（惯性测量单元，通常为加速度计和陀螺仪）的数据。这类时序数据在输入机器学习模型训练前需要进行预处理，这也是嵌入式机器学习中的一大难点。Edge Impulse 通过其数字信号处理（DSP）预处理步骤，尤其是针对惯性传感器的频谱特征模块，帮助我们简化了这一复杂过程。

那么它的底层原理是什么？让我们深入了解一下。

特征提取回顾

从惯性传感器（如加速度计）采集的数据中提取特征，涉及对原始数据的处理与分析。加速度计测量物体在一个或多个轴（通常为 X、Y、Z 三轴）上的加速度，这些测量值可用于分析物体的运动模式和振动特性。以下是高层次的处理流程：

数据采集：首先需要从加速度计采集数据。根据应用场景，采样率可能不同。采样率必须足够高，以捕捉运动中的关键动态（采样率应至少为信号中最高相关频率的两倍）。

数据预处理：原始加速度计数据可能包含噪声、误差或无关信息。通过滤波、归一化等预处理步骤，可以清洗和标准化数据，使其更适合后续特征提取。

Studio 不会自动进行归一化或标准化，因此在进行传感器融合（Sensor Fusion）时，有时需要在上传数据前手动完成这一步。这在传感器融合项目中尤为重要，详见本教程： Sensor Data Fusion with Spresense and CommonSense 。

分段处理：根据数据和应用需求，通常需要将数据划分为更小的片段或窗口。这样可以聚焦于数据集中的特定事件或活动，使特征提取更具针对性和意义。窗口大小及重叠（窗口跨度）的选择取决于应用和关注事件的频率。一般建议窗口能覆盖几个“数据周期”。

特征提取：数据预处理和分段后，可以提取描述运动特征的特征。常见的加速度计特征包括：

时域特征：描述每个片段内数据的统计属性，如均值、中位数、标准差、偏度、峰度、过零率等。
频域特征：通过如快速傅里叶变换（FFT）等方法将数据转换到频域，常见特征有功率谱、谱能量、主频（幅值和频率）、谱熵等。
时频域特征：结合时域和频域信息，如短时傅里叶变换（STFT）或离散小波变换（DWT），可更细致地分析信号频率随时间的变化。

在许多情况下，提取的特征数量可能很大，导致过拟合或计算复杂度增加。可以采用特征选择技术（如互信息、相关性分析或主成分分析 PCA）筛选最相关特征，降低数据维度。Studio 也能辅助完成相关特征筛选。

下面我们以本系列 Hands-ON 覆盖的典型 TinyML 运动分类项目为例，进一步探讨。

一个 TinyML 运动分类项目

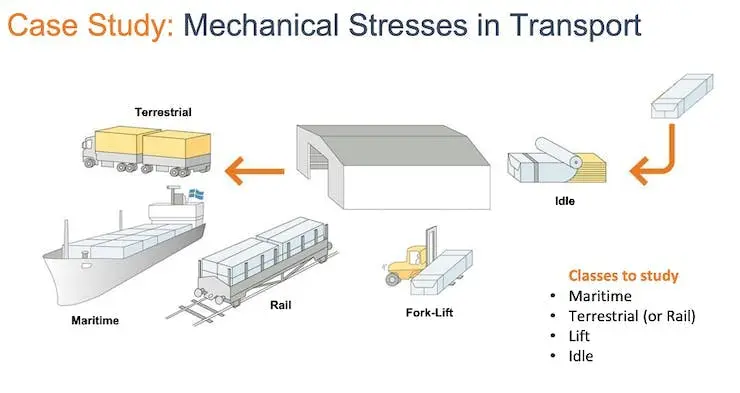
在实践项目“运动分类与异常检测”中，我们模拟了运输过程中的机械应力，目标是对四种运动状态进行分类：

海运（托盘在船上）
陆运（托盘在卡车或火车上）
升降（托盘被叉车搬运）
静止（托盘在仓库中）

加速度计为托盘（或集装箱）提供了运动数据。

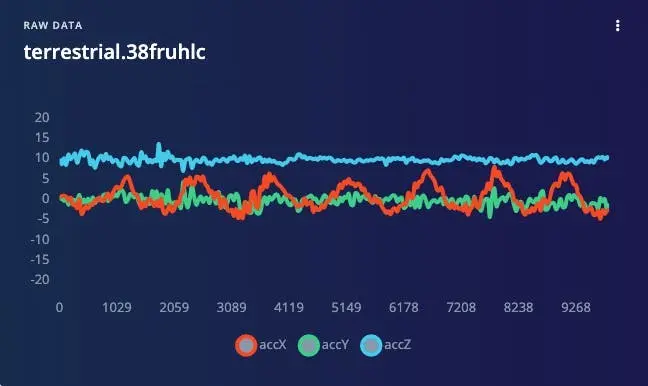
下图为采样频率 50 Hz、时长 10 秒的一组原始数据样本：

若采用不同采样率（如 62.5 Hz），分析结果与上述原理类似。

数据预处理

加速度计采集的原始数据（时序数据）需通过典型特征提取方法转化为“表格数据”。

我们应采用滑动窗口对样本数据进行分段以提取特征。项目中每 10 秒采集一次加速度数据，采样率为 62.5 Hz。2 秒窗口包含 375 个数据点（3 轴 × 2 秒 × 62.5 次采样）。窗口每 80 ms 滑动一次，生成更大的数据集，每个实例有 375 个“原始特征”。

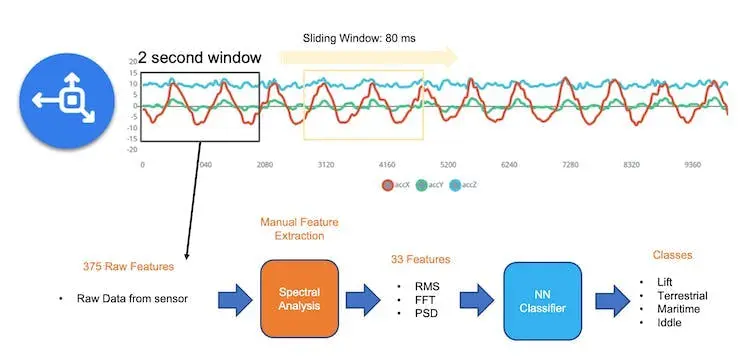
在 Studio 的早期版本（V1）中，频谱分析模块仅提取了时域 RMS，频域则提取了信号的峰值、主频（通过 FFT）和功率特征（PSD），最终每轴生成 11 个特征，共 33 个特征，形成固定表格数据集。

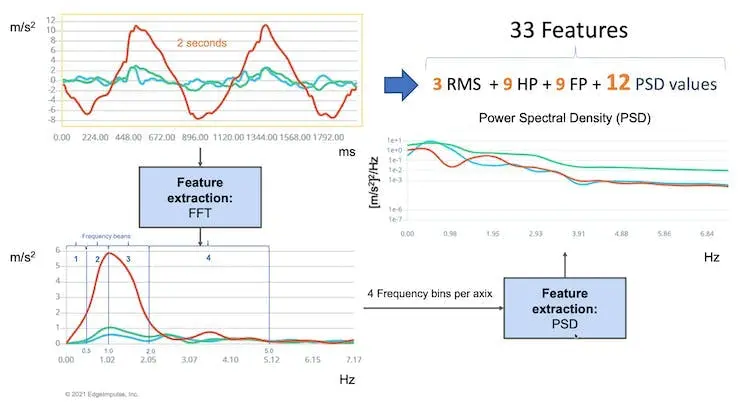
这 33 个特征作为神经网络分类器的输入张量。

2022 年，Edge Impulse 发布了频谱分析模块的第二版（V2），我们将在下文详细介绍。

Edge Impulse 频谱分析模块 V2 原理

V2 版本中，每个通道/轴的时域统计特征包括：

RMS
偏度（Skewness）
峰度（Kurtosis）

频域谱特征包括：

谱功率（Spectral Power）
偏度（Skewness，后续版本支持）
峰度（Kurtosis，后续版本支持）

更多特征提取细节可参考官方文档。

可克隆公开项目。也可参考我的 Google CoLab Notebook，边看边实践： Edge Impulse Spectral Analysis Block Notebook 。

首先导入相关库：

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import math
from scipy.stats import skew, kurtosis
from scipy import signal
from scipy.signal import welch
from scipy.stats import entropy
from sklearn import preprocessing
import pywt

plt.rcParams['figure.figsize'] = (12, 6)
plt.rcParams['lines.linewidth'] = 3

以项目中的加速度计数据样本为例：

窗口大小 2 秒：[2,000] ms
采样频率：[62.5] Hz
滤波器选择 [None]（为简化）
FFT 长度：[16]

f =  62.5 # 赫兹
wind_sec = 2 # 秒
FFT_Lenght = 16
axis = ['accX', 'accY', 'accZ']
n_sensors = len(axis)

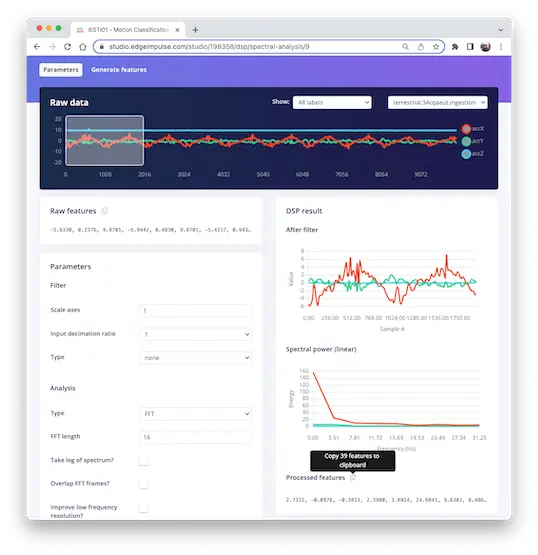
在 Studio 的 Spectral Analysis 标签页选择 Raw Features，可复制某 2 秒窗口的全部 375 个数据点。

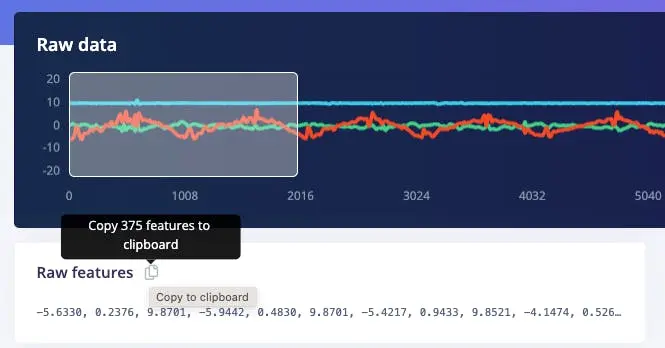
将数据粘贴到变量 data：

data = [
    -5.6330,  0.2376,  9.8701,
    -5.9442,  0.4830,  9.8701,
    -5.4217, ...
]
No_raw_features = len(data)
N = int(No_raw_features/n_sensors)

总原始特征为 375 个，但我们将分别处理每个轴的数据，即 $N=125$（每轴样本数）。

我们的目标是理解 Edge Impulse 如何生成处理后的特征。

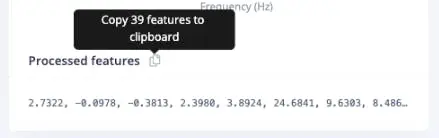
同样，将处理后的特征粘贴到变量中（便于与 Python 计算结果对比）：

features = [
    2.7322, -0.0978, -0.3813,
    2.3980, 3.8924, 24.6841,
    9.6303, ...
]
N_feat = len(features)
N_feat_axis = int(N_feat/n_sensors)

总处理特征为 39 个，即每轴 13 个特征。

细看这 13 个特征，时域有 3 个（RMS、偏度、峰度）：

[rms] [skew] [kurtosis]

频域有 10 个（后文详述）：

[spectral skew][spectral kurtosis][Spectral Power 1] ... [Spectral Power 8]

按传感器轴拆分原始数据

数据包含所有轴的样本，需分别拆分并绘图：

def plot_data(sensors, axis, title):
    [plt.plot(x, label=y) for x,y in zip(sensors, axis)]
    plt.legend(loc='lower right')
    plt.title(title)
    plt.xlabel('#Sample')
    plt.ylabel('Value')
    plt.box(False)
    plt.grid()
    plt.show()

accX = data[0::3]
accY = data[1::3]
accZ = data[2::3]
sensors = [accX, accY, accZ]
plot_data(sensors, axis, 'Raw Features')

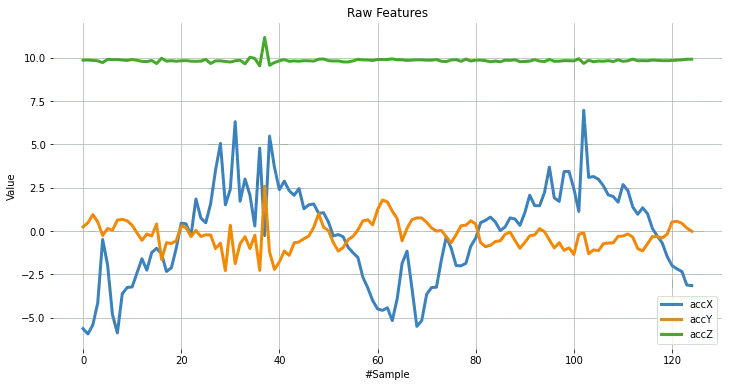
去均值处理

接下来需对 data 去均值。去均值是统计和机器学习中常见的预处理步骤，目的是将数据中心化，有助于揭示隐藏的模式和关系。

去均值的好处包括：

简化分析：中心化后均值为零，部分计算更简便。
消除偏差：去除数据偏置，分析更准确。
揭示模式：中心化有助于发现时序数据中的趋势。
提升算法表现：部分算法对中心化数据表现更佳，减少异常值影响。

dtmean = [
    (sum(x) / len(x))
    for x in sensors
]

[
    print('mean_' + x + ' =', round(y, 4))
    for x, y in zip(axis, dtmean)
][0]

accX = [(x - dtmean[0]) for x in accX]
accY = [(x - dtmean[1]) for x in accY]
accZ = [(x - dtmean[2]) for x in accZ]
sensors = [accX, accY, accZ]

plot_data(sensors, axis, 'Raw Features - Subctract the Mean')

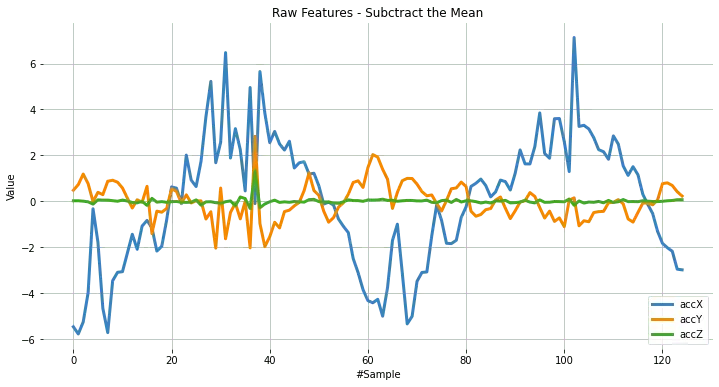
时域统计特征

RMS 计算

RMS（均方根）是数值集合（或连续波形）平方后取平均再开方的结果。在物理学中，电流的 RMS 值定义为“在电阻上消耗相同功率的直流电流值”。

对于 $n$ 个值 ${𝑥_1, 𝑥_2, \ldots, 𝑥_𝑛}$，RMS 计算公式为： $$ x_{\mathrm{RMS}} = \sqrt{\frac{1}{n} \left( x_1^2 + x_2^2 + \cdots + x_n^2 \right)} $$

注意：原始数据和去均值后的 RMS 值不同

# 使用 numpy 计算去均值后的 RMS
rms = [np.sqrt(np.mean(np.square(x))) for x in sensors]

可将计算结果与 Edge Impulse 的特征对比：

[print('rms_'+x+'= ', round(y, 4)) for x,y in zip(axis, rms)][0]
print("\nCompare with Edge Impulse result features")
print(features[0:N_feat:N_feat_axis])

rms_accX= 2.7322

rms_accY= 0.7833

rms_accZ= 0.1383

Edge Impulse 结果：

[2.7322, 0.7833, 0.1383]

偏度与峰度计算

在统计学中，偏度和峰度用于衡量分布的形态。

下图展示了各轴数据的分布：

fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(13, 4))
sns.kdeplot(accX, fill=True, ax=axes[0])
sns.kdeplot(accY, fill=True, ax=axes[1])
sns.kdeplot(accZ, fill=True, ax=axes[2])
axes[0].set_title('accX')
axes[1].set_title('accY')
axes[2].set_title('accZ')
plt.suptitle('IMU Sensors distribution', fontsize=16, y=1.02)
plt.show()

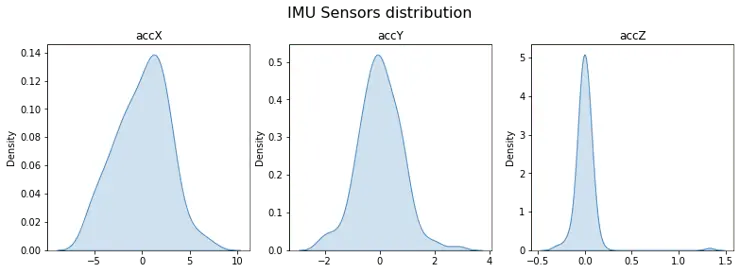
偏度衡量分布的不对称性，可为正或负。

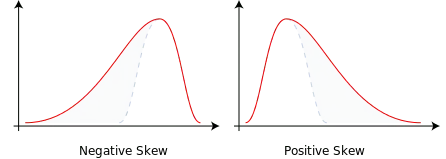
负偏度：分布左侧尾部较长，向负值延伸。
正偏度：分布右侧尾部较长，向正值延伸。
零偏度：分布完全对称。

skew = [skew(x, bias=False) for x in sensors]
[print('skew_'+x+'= ', round(y, 4))
  for x,y in zip(axis, skew)][0]
print("\nCompare with Edge Impulse result features")
features[1:N_feat:N_feat_axis]

skew_accX= -0.099

skew_accY= 0.1756

skew_accZ= 6.9463

Edge Impulse 结果：

[-0.0978, 0.1735, 6.8629]

峰度衡量分布相较于正态分布的尾部厚度。

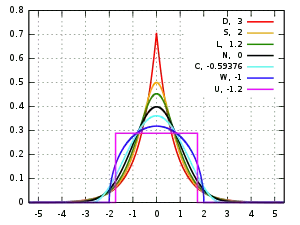
正态分布峰度为零。
负峰度（扁峰）：极端值较少。
正峰度（尖峰）：极端值较多。

kurt = [kurtosis(x, bias=False) for x in sensors]
[print('kurt_'+x+'= ', round(y, 4))
  for x,y in zip(axis, kurt)][0]
print("\nCompare with Edge Impulse result features")
features[2:N_feat:N_feat_axis]

kurt_accX= -0.3475

kurt_accY= 1.2673

kurt_accZ= 68.1123

Edge Impulse 结果：

[-0.3813, 1.1696, 65.3726]

频谱特征

滤波后的信号会进入频谱功率计算环节，通过FFT生成频谱特征。

由于采样窗口通常大于 FFT 大小，窗口会被分割为多个帧（子窗口），每帧做一次 FFT。

FFT 长度决定 FFT bin 数量和频率分辨率。较小的 FFT 长度会将更多信号平均到同一 bin，特征和模型体积较小；较大长度则能分辨更多频率，特征和模型体积也更大。

谱功率特征数量取决于滤波和 FFT 参数。无滤波时，特征数为 FFT 长度的一半。

谱功率 - Welch 方法

应采用 Welch 方法将信号分割为频域 bin 并计算每个 bin 的功率谱。该方法将信号分段、加窗、对每段做 DFT 并取平均，得到更平滑的功率谱估计。

# Edge Impulse 使用的 Welch 变体
def welch_max_hold(fx, sampling_freq, nfft, n_overlap):
    n_overlap = int(n_overlap)
    spec_powers = [0 for _ in range(nfft//2+1)]
    ix = 0
    while ix <= len(fx):
        # Slicing truncates if end_idx > len,
        # and rfft will auto-zero pad
        fft_out = np.abs(np.fft.rfft(fx[ix:ix+nfft], nfft))
        spec_powers = np.maximum(spec_powers, fft_out**2/nfft)
        ix = ix + (nfft-n_overlap)
    return np.fft.rfftfreq(nfft, 1/sampling_freq), spec_powers

对三轴信号应用上述函数：

fax,Pax = welch_max_hold(accX, fs, FFT_Lenght, 0)
fay,Pay = welch_max_hold(accY, fs, FFT_Lenght, 0)
faz,Paz = welch_max_hold(accZ, fs, FFT_Lenght, 0)
specs = [Pax, Pay, Paz ]

绘制功率谱 P(f)：

plt.plot(fax,Pax, label='accX')
plt.plot(fay,Pay, label='accY')
plt.plot(faz,Paz, label='accZ')
plt.legend(loc='upper right')
plt.xlabel('Frequency (Hz)')
#plt.ylabel('PSD [V**2/Hz]')
plt.ylabel('Power')
plt.title('Power spectrum P(f) using Welch\'s method')
plt.grid()
plt.box(False)
plt.show()

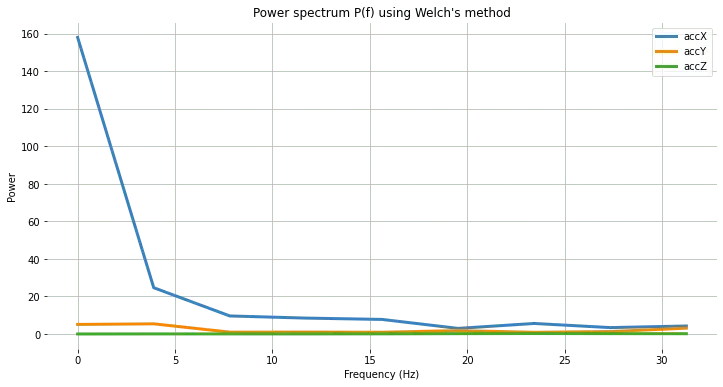
除功率谱外，还可计算频域特征的偏度和峰度（新版本支持）：

spec_skew = [skew(x, bias=False) for x in specs]
spec_kurtosis = [kurtosis(x, bias=False) for x in specs]

列出各轴频谱特征并与 EI 对比：

print("EI Processed Spectral features (accX): ")
print(features[3:N_feat_axis][0:])
print("\nCalculated features:")
print (round(spec_skew[0],4))
print (round(spec_kurtosis[0],4))
[print(round(x, 4)) for x in Pax[1:]][0]

EI 处理后 accX 频谱特征：

2.398, 3.8924, 24.6841, 9.6303, 8.4867, 7.7793, 2.9963, 5.6242, 3.4198, 4.2735

Python 计算结果：

2.9069 8.5569 24.6844 9.6304 8.4865 7.7794 2.9964 5.6242 3.4198 4.2736

print("EI Processed Spectral features (accY): ")
print(features[16:26][0:]) # 13: 3+N_feat_axis;
                           # 26 = 2x N_feat_axis
print("\nCalculated features:")
print (round(spec_skew[1],4))
print (round(spec_kurtosis[1],4))
[print(round(x, 4)) for x in Pay[1:]][0]

EI 处理后 accY 频谱特征：

0.9426, -0.8039, 5.429, 0.999, 1.0315, 0.9459, 1.8117, 0.9088, 1.3302, 3.112

Python 计算结果：

1.1426 -0.3886 5.4289 0.999 1.0315 0.9458 1.8116 0.9088 1.3301 3.1121

print("EI Processed Spectral features (accZ): ")
print(features[29:][0:]) #29: 3+(2*N_feat_axis);
print("\nCalculated features:")
print (round(spec_skew[2],4))
print (round(spec_kurtosis[2],4))
[print(round(x, 4)) for x in Paz[1:]][0]

EI 处理后 accZ 频谱特征：

0.3117, -1.3812, 0.0606, 0.057, 0.0567, 0.0976, 0.194, 0.2574, 0.2083, 0.166

Python 计算结果：

0.3781 -1.4874 0.0606 0.057 0.0567 0.0976 0.194 0.2574 0.2083 0.166

时频域特征

小波分析

小波变换是分析具有瞬态特征或突变（如尖峰、边缘）信号的强大工具，传统傅里叶方法难以处理这类信号。

小波变换通过将信号分解为不同频率分量并分别分析实现。其本质是用小波函数（在特定时间和频率中心的短波形）对信号进行卷积，将信号分解为不同频带，便于分别分析。

小波变换的关键优势在于支持时频分析，即能揭示信号频率随时间的变化，特别适合分析非平稳信号。

小波广泛应用于信号/图像压缩、去噪、特征提取和图像处理等领域。

在 Spectral Features 模块选择 Wavelet：

类型：Wavelet
分解层数：1
小波类型：bior1.3

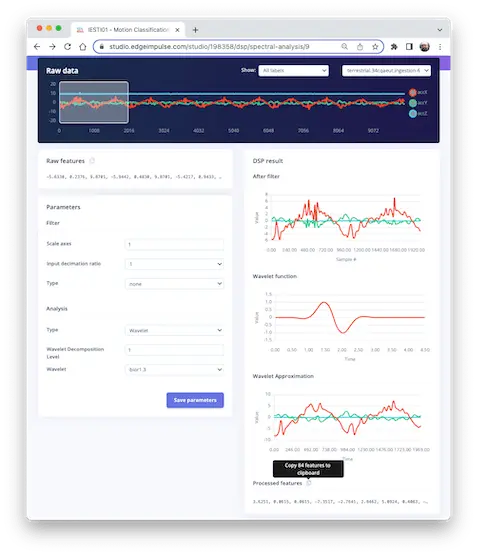
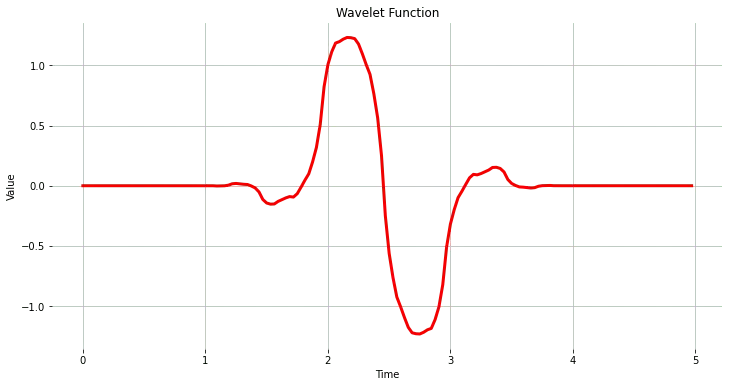
小波函数

wavelet_name='bior1.3'
num_layer = 1

wavelet = pywt.Wavelet(wavelet_name)
[phi_d,psi_d,phi_r,psi_r,x] = wavelet.wavefun(level=5)
plt.plot(x, psi_d, color='red')
plt.title('Wavelet Function')
plt.ylabel('Value')
plt.xlabel('Time')
plt.grid()
plt.box(False)
plt.show()

同样复制处理后特征：

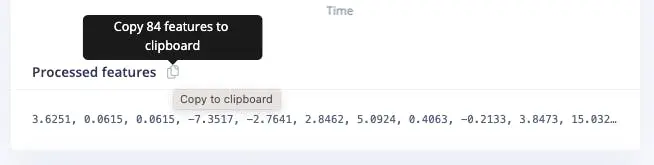
features = [
    3.6251, 0.0615, 0.0615,
    -7.3517, -2.7641, 2.8462,
    5.0924, ...
]
N_feat = len(features)
N_feat_axis = int(N_feat/n_sensors)

Edge Impulse 对每个小波分解层执行离散小波变换（DWT），然后提取特征。

对于小波，提取的特征包括基本统计量、过零/均值穿越和熵，每层共 14 个特征：

[11] 统计特征：n5, n25, n75, n95, 均值，中位数，标准差，方差，RMS, 峰度，偏度
[2] 穿越特征：过零率（zcross）、均值穿越率（mcross），分别表示信号穿越零线和均值线的次数
[1] 复杂度特征：熵，衡量信号复杂度

上述 14 个特征对每层（含 L0 原始信号）均计算

特征总数取决于滤波和层数。例如无滤波、Level[1] 时，每轴 $14\times 2$（L0+L1）= 28，总计 84 个特征（三轴）。

小波分析

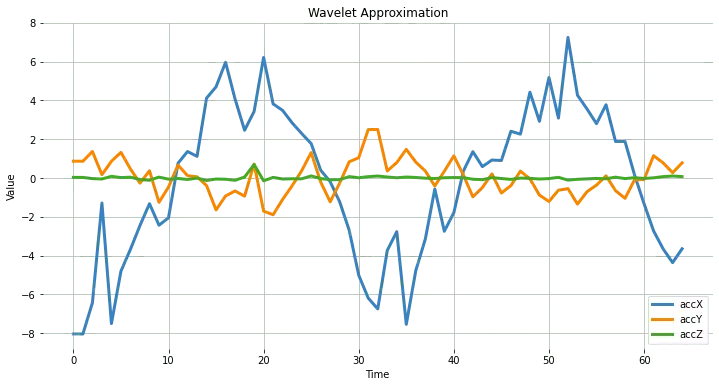
小波分析将信号（accX, accY, accZ）分解为不同频率分量，分别提取低频（长期模式，如 accX_l1, accY_l1, accZ_l1）和高频（短期模式，如 accX_d1, accY_d1, accZ_d1）分量，便于后续特征提取和分类。

这里只用低频分量（近似系数 cA）。单层分解时，函数返回元组；多层分解时返回列表，详见离散小波变换 DWT 。

(accX_l1, accX_d1) = pywt.dwt(accX, wavelet_name)
(accY_l1, accY_d1) = pywt.dwt(accY, wavelet_name)
(accZ_l1, accZ_d1) = pywt.dwt(accZ, wavelet_name)
sensors_l1 = [accX_l1, accY_l1, accZ_l1]

# 绘制近似分量
plt.plot(accX_l1, label='accX')
plt.plot(accY_l1, label='accY')
plt.plot(accZ_l1, label='accZ')
plt.legend(loc='lower right')
plt.xlabel('Time')
plt.ylabel('Value')
plt.title('Wavelet Approximation')
plt.grid()
plt.box(False)
plt.show()

特征提取

先提取基本统计特征，对原始信号和 DWT 近似分量均适用：

def calculate_statistics(signal):
    n5 = np.percentile(signal, 5)
    n25 = np.percentile(signal, 25)
    n75 = np.percentile(signal, 75)
    n95 = np.percentile(signal, 95)
    median = np.percentile(signal, 50)
    mean = np.mean(signal)
    std = np.std(signal)
    var = np.var(signal)
    rms = np.sqrt(np.mean(np.square(signal)))
    return [n5, n25, n75, n95, median, mean, std, var, rms]

stat_feat_l0 = [calculate_statistics(x) for x in sensors]
stat_feat_l1 = [calculate_statistics(x) for x in sensors_l1]

偏度与峰度：

skew_l0 = [skew(x, bias=False) for x in sensors]
skew_l1 = [skew(x, bias=False) for x in sensors_l1]
kurtosis_l0 = [kurtosis(x, bias=False) for x in sensors]
kurtosis_l1 = [kurtosis(x, bias=False) for x in sensors_l1]

过零率（zcross）：信号穿越零轴的次数，反映频率成分，高频信号过零多。

均值穿越率（mcross）：信号穿越均值线的次数，反映幅度特性，高幅值信号均值穿越多。

def getZeroCrossingRate(arr):
    my_array = np.array(arr)
    zcross = float(
        "{:.2f}".format(
          (((my_array[:-1] * my_array[1:]) < 0).sum()) / len(arr)
        )
    )
    return zcross

def getMeanCrossingRate(arr):
    mcross = getZeroCrossingRate(np.array(arr) - np.mean(arr))
    return mcross

def calculate_crossings(list):
    zcross=[]
    mcross=[]
    for i in range(len(list)):
        zcross_i = getZeroCrossingRate(list[i])
        zcross.append(zcross_i)
        mcross_i = getMeanCrossingRate(list[i])
        mcross.append(mcross_i)
    return zcross, mcross

cross_l0 = calculate_crossings(sensors)
cross_l1 = calculate_crossings(sensors_l1)

小波分析中的熵衡量小波系数分布的无序度或复杂度。这里用 Shannon 熵，值越大信号越复杂。

def calculate_entropy(signal, base=None):
    value, counts = np.unique(signal, return_counts=True)
    return entropy(counts, base=base)

entropy_l0 = [calculate_entropy(x) for x in sensors]
entropy_l1 = [calculate_entropy(x) for x in sensors_l1]

最后，汇总所有小波特征并按层组织：

L1_features_names = [
    "L1-n5", "L1-n25", "L1-n75", "L1-n95", "L1-median",
    "L1-mean", "L1-std", "L1-var", "L1-rms", "L1-skew",
    "L1-Kurtosis", "L1-zcross", "L1-mcross", "L1-entropy"
]

L0_features_names = [
    "L0-n5", "L0-n25", "L0-n75", "L0-n95", "L0-median",
    "L0-mean", "L0-std", "L0-var", "L0-rms", "L0-skew",
    "L0-Kurtosis", "L0-zcross", "L0-mcross", "L0-entropy"
]

all_feat_l0 = []
for i in range(len(axis)):
    feat_l0 = (
        stat_feat_l0[i]
        + [skew_l0[i]]
        + [kurtosis_l0[i]]
        + [cross_l0[0][i]]
        + [cross_l0[1][i]]
        + [entropy_l0[i]]
    )
    [print(axis[i] + ' +x+= ', round(y, 4))
       for x, y in zip(LO_features_names, feat_l0)][0]
    all_feat_l0.append(feat_l0)

all_feat_l0 = [
    item
    for sublist in all_feat_l0
    for item in sublist
]
print(f"\nAll L0 Features = {len(all_feat_l0)}")

all_feat_l1 = []
for i in range(len(axis)):
    feat_l1 = (
        stat_feat_l1[i]
        + [skew_l1[i]]
        + [kurtosis_l1[i]]
        + [cross_l1[0][i]]
        + [cross_l1[1][i]]
        + [entropy_l1[i]]
    )
    [print(axis[i]+' '+x+'= ', round(y, 4))
       for x,y in zip(L1_features_names, feat_l1)][0]
    all_feat_l1.append(feat_l1)

all_feat_l1 = [
    item
    for sublist in all_feat_l1
    for item in sublist
]
print(f"\nAll L1 Features = {len(all_feat_l1)}")

总结

Edge Impulse Studio 是一个强大的在线平台，可以为我们自动完成预处理任务。但从工程师视角出发，理解底层原理有助于我们为项目选择最佳方案和超参数。

Daniel Situnayake 在其博客中写道：“原始传感器数据维度高且噪声大。数字信号处理算法帮助我们从噪声中提取信号。DSP 是嵌入式工程的核心，许多边缘处理器都内置了 DSP 加速。作为 ML 工程师，掌握基础 DSP 能力将极大提升你处理高频时序数据的能力。”强烈推荐阅读 Dan 的精彩博文： nn to cpp: What you need to know about porting deep learning models to the edge 。

发布于: 2025/10/22 • 最后更新: 2025/10/22 • 字数: 4947 • 阅读时间: 10 mins